Source: Principles of Physics
Problem
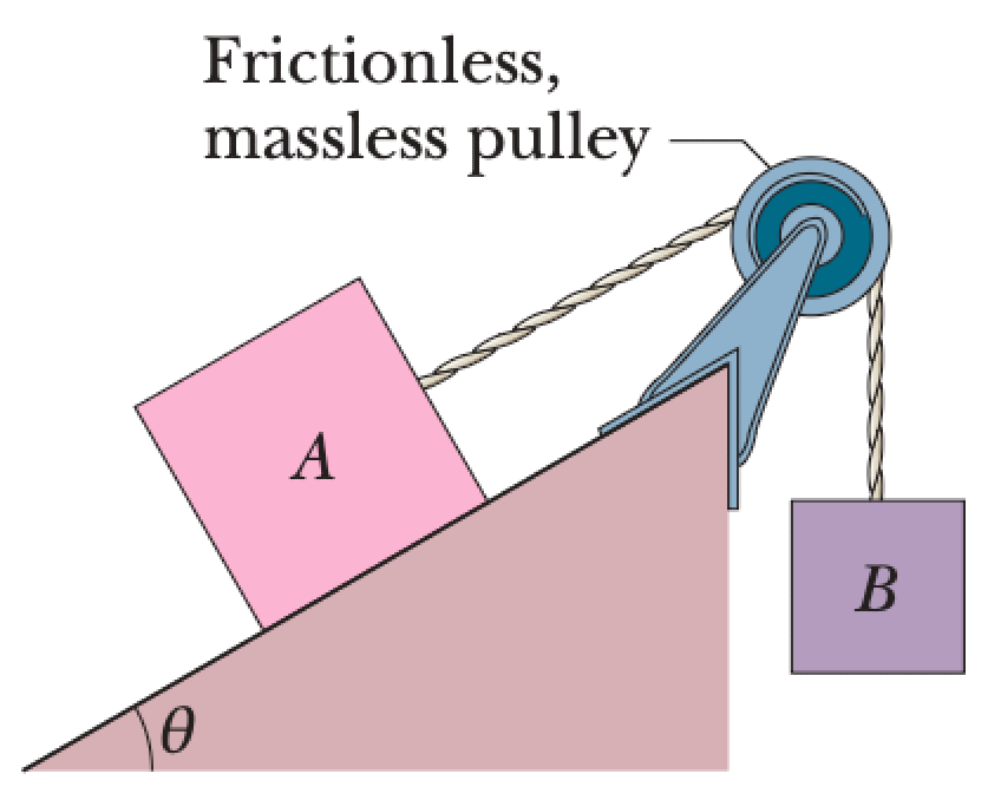
A block of mass $m_A$ on an inclined plane at angle $\theta$ is connected by a rope over a frictionless, massless pulley to a hanging block of mass $m_B$. The coefficients of static and kinetic friction between block A and the incline are $\mu_s$ and $\mu_k$. The positive direction is defined as up the incline, represented by the unit vector $\hat{i}$.
- In unit-vector notation, what is the acceleration of A if A is initially at rest?
- In unit-vector notation, what is the acceleration of A if A is initially moving up the incline?
- In unit-vector notation, what is the acceleration of A if A is initially moving down the incline?
01K63JS7AVRX6H1QGWP9AJW76G
[Q1] $\vec{a} = 0$, provided that $|m_B - m_A \sin\theta| \le \mu_s m_A \cos\theta$. [Q2] $\vec{a} = \frac{g(m_B - m_A(\sin\theta + \mu_k \cos\theta))}{m_A + m_B} \hat{i}$ [Q3] $\vec{a} = \frac{g(m_B - m_A(\sin\theta - \mu_k \cos\theta))}{m_A + m_B} \hat{i}$
Let $a$ be the acceleration of the system up the incline. We apply Newton's second law to the entire system of total mass $M = m_A + m_B$. The forces acting along the incline are the gravitational force from block B ($m_B g$), the parallel component of gravity on block A ($m_A g \sin\theta$), and the friction force $f$ on block A. The normal force on A is $N = m_A g \cos\theta$.
[Q1] If the system is initially at rest, it remains at rest if the net force from gravity is less than or equal to the maximum static friction force, $f_{s,max} = \mu_s N$. The condition for static equilibrium is:
$$|m_B g - m_A g \sin\theta| \le \mu_s m_A g \cos\theta$$If this condition holds, the static friction force balances the other forces, and the acceleration is zero.
[Q2] If A is moving up the incline, kinetic friction $f_k = \mu_k N = \mu_k m_A g \cos\theta$ acts down the incline, opposing motion. The net force equation for the system is:
$$F_{net} = m_B g - m_A g \sin\theta - f_k = (m_A + m_B)a$$Solving for acceleration $a$:
$$a = \frac{g(m_B - m_A \sin\theta - \mu_k m_A \cos\theta)}{m_A + m_B}$$[Q3] If A is moving down the incline, kinetic friction $f_k$ acts up the incline, opposing motion. The net force equation is:
$$F_{net} = m_B g - m_A g \sin\theta + f_k = (m_A + m_B)a$$Solving for acceleration $a$:
$$a = \frac{g(m_B - m_A \sin\theta + \mu_k m_A \cos\theta)}{m_A + m_B}$$The acceleration vector is $\vec{a} = a \hat{i}$.