Source: Principles of Physics
Problem
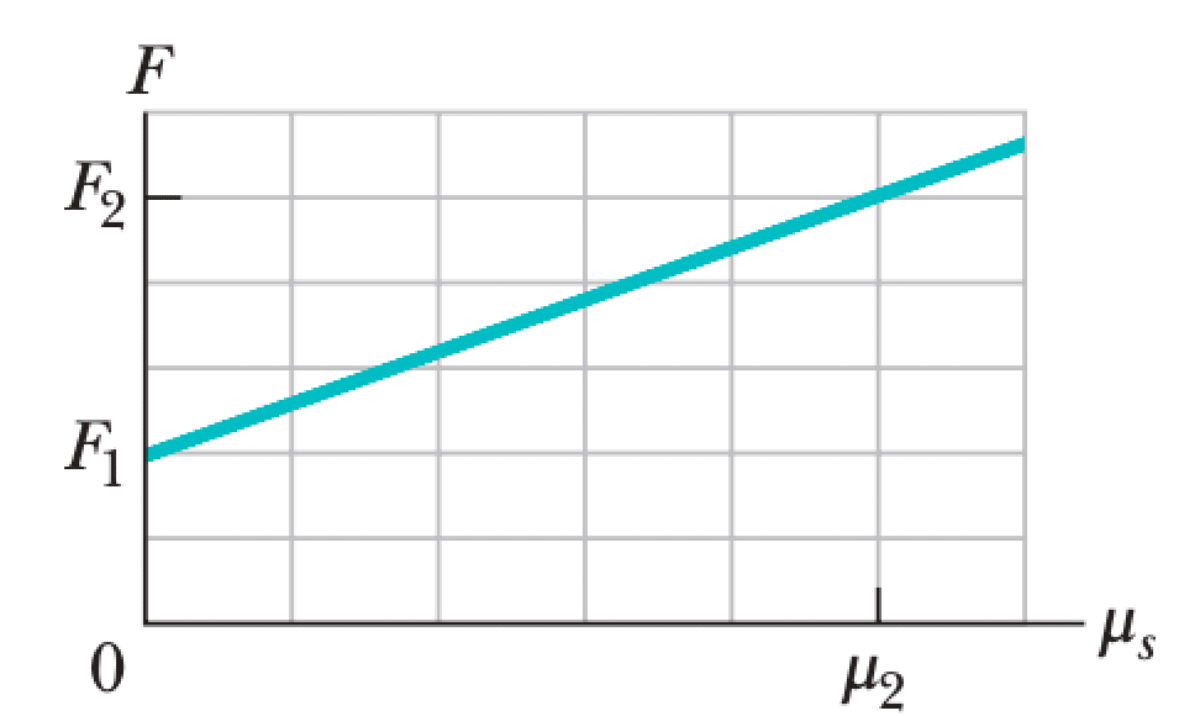
A sled is held on an inclined plane by a cord pulling up the plane. The sled is on the verge of moving up the plane. The magnitude $F$ of the cord's force is a linear function of the coefficient of static friction $\mu_s$. The data shows that the force is $F_1$ when $\mu_s = 0$, and the force is $F_2$ when $\mu_s = \mu_{s2}$.
01K63JKB663CTVF9GYV36J3NE0
Let the sled have weight $W$. We apply Newton's first law by resolving forces parallel ($\hat{x}$) and perpendicular ($\hat{y}$) to the incline.
The sum of forces perpendicular to the incline is zero:
$$ \sum F_y = N - W\cos\theta = 0 \implies N = W\cos\theta $$Since the sled is on the verge of moving up the incline, the maximum static friction force $f_s = \mu_s N$ acts down the incline. The sum of forces parallel to the incline is also zero:
$$ \sum F_x = F - W\sin\theta - f_s = 0 $$Substituting $f_s = \mu_s N = \mu_s W\cos\theta$ and solving for $F$ gives a linear relationship:
$$ F(\mu_s) = W\sin\theta + \mu_s (W\cos\theta) $$This equation is of the form $y = b + mx$, where $F$ is $y$ and $\mu_s$ is $x$. The y-intercept ($F$ at $\mu_s = 0$) is given as $F_1$.
$$ F_1 = W\sin\theta $$The slope is $m = W\cos\theta$. We can find the slope from the two data points $(0, F_1)$ and $(\mu_{s2}, F_2)$:
$$ m = \frac{\Delta F}{\Delta \mu_s} = \frac{F_2 - F_1}{\mu_{s2} - 0} = W\cos\theta $$To find $\theta$, divide the expression for $F_1$ by the expression for the slope:
$$ \frac{W\sin\theta}{W\cos\theta} = \tan\theta = \frac{F_1}{(F_2 - F_1) / \mu_{s2}} $$ $$ \tan\theta = \frac{F_1 \mu_{s2}}{F_2 - F_1} $$