Source: Principles of Physics
Problem
Two boxes of mass $m_1$ and $m_2$ are in contact on a horizontal surface. A horizontal force $\vec{F}$ is applied to the first box, $m_1$. The frictional forces on the boxes are $f_1$ and $f_2$, respectively.
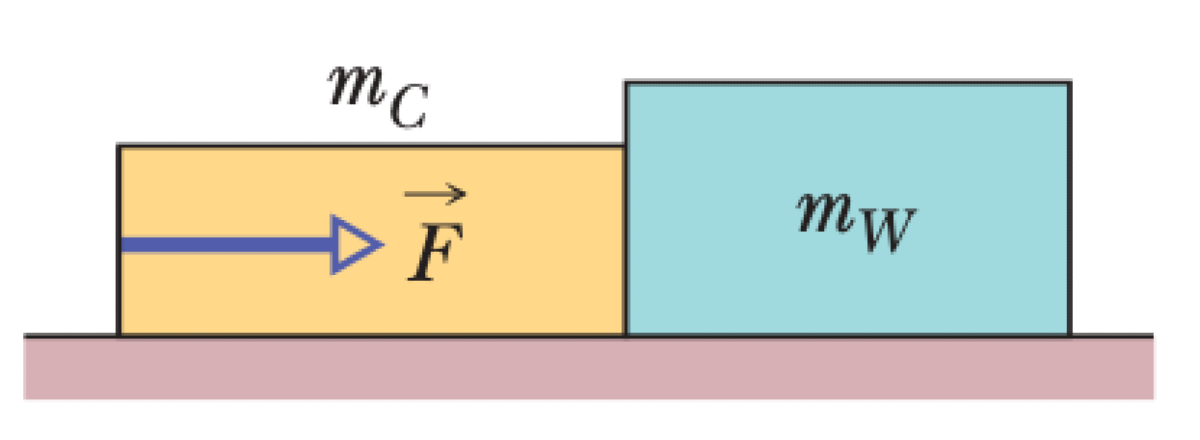
01K63JHY1XPTMYW6PMGQR11KMW
First, consider the two boxes as a single system with total mass $M = m_1 + m_2$. The net external force on the system is the applied force minus the total friction, $F_{net} = F - f_1 - f_2$.
Applying Newton's second law to the system gives the common acceleration $a$:
$$F - f_1 - f_2 = (m_1 + m_2)a$$ $$a = \frac{F - f_1 - f_2}{m_1 + m_2}$$Next, isolate box $m_2$. The forces acting on it in the horizontal direction are the contact force from box 1, $F_{12}$, and the frictional force $f_2$. Applying Newton's second law to box $m_2$:
$$F_{12} - f_2 = m_2 a$$Solving for $F_{12}$ and substituting the expression for $a$:
$$F_{12} = m_2 a + f_2 = m_2 \left( \frac{F - f_1 - f_2}{m_1 + m_2} \right) + f_2$$To simplify, find a common denominator:
$$F_{12} = \frac{m_2(F - f_1 - f_2) + f_2(m_1 + m_2)}{m_1 + m_2}$$ $$F_{12} = \frac{m_2 F - m_2 f_1 - m_2 f_2 + m_1 f_2 + m_2 f_2}{m_1 + m_2}$$ $$F_{12} = \frac{m_2 F - m_2 f_1 + m_1 f_2}{m_1 + m_2}$$