Source: Principles of Physics
Problem
A horizontal force $\vec{F}$ pushes a block of weight $W$ against a vertical wall. The block is initially at rest. The coefficient of static friction between the wall and the block is $\mu_s$. The coordinate system is defined with the x-axis horizontal (positive in the direction of $\vec{F}$) and the y-axis vertical (positive upwards).
- Under what condition will the block remain stationary?
- Assuming the block remains stationary, what is the force exerted by the wall on the block, $\vec{F}_{wall}$, in unit-vector notation?
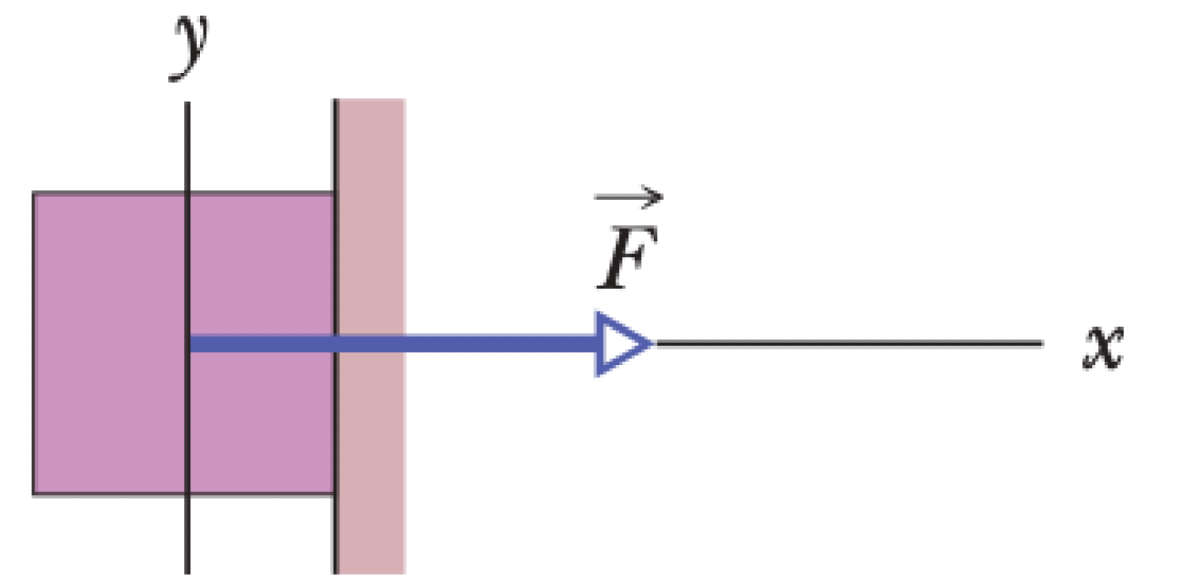
01K63JGRF6JHPSS4HB5GSTFC7P
[Q1] $W \le \mu_s F$ [Q2] $\vec{F}_{wall} = -F\hat{i} + W\hat{j}$
We analyze the forces and apply Newton's first law for static equilibrium, as the block is assumed to be stationary. The forces acting on the block are the applied force $\vec{F}$, weight $\vec{W}$, normal force from the wall $\vec{N}$, and static friction $\vec{f}_s$.
In the horizontal direction (x-axis), the applied force is balanced by the normal force from the wall:
$$\sum F_x = F - N = 0 \implies N = F$$In the vertical direction (y-axis), the static friction force opposes the weight of the block. For the block to remain stationary, the static friction required must be less than or equal to the maximum possible static friction, $f_{s,max}$.
$$f_{s,max} = \mu_s N$$Substituting $N=F$, we get:
$$f_{s,max} = \mu_s F$$The downward force is the block's weight, $W$. The condition for the block to remain stationary is that the weight does not exceed the maximum static friction.
$$W \le f_{s,max} \implies W \le \mu_s F$$If the block is stationary, the total force from the wall, $\vec{F}_{wall}$, is the vector sum of the normal force $\vec{N}$ and the static friction force $\vec{f}_s$. The normal force acts in the negative x-direction: $\vec{N} = -N\hat{i} = -F\hat{i}$. For vertical equilibrium, the friction force must balance the weight:
$$\sum F_y = f_s - W = 0 \implies f_s = W$$The friction force acts in the positive y-direction: $\vec{f}_s = W\hat{j}$.
The total force from the wall is:
$$\vec{F}_{wall} = \vec{N} + \vec{f}_s = -F\hat{i} + W\hat{j}$$