Source: Principles of Physics
Problem
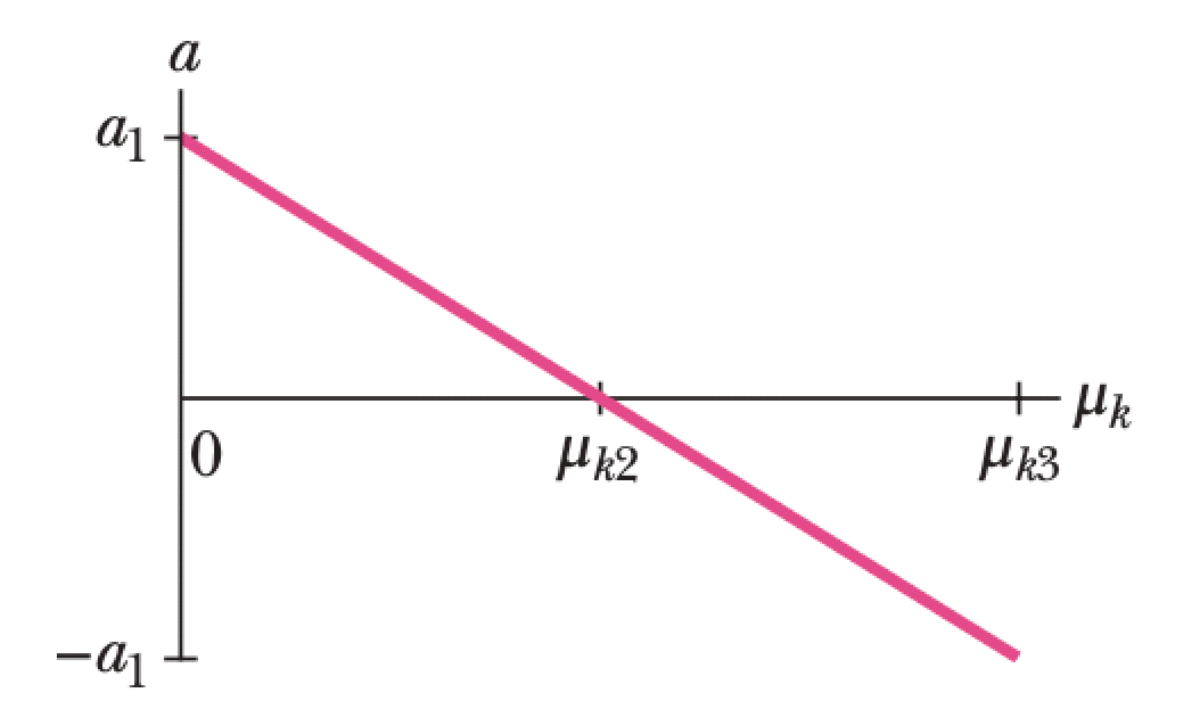
A block of mass $m$ is pushed across a floor by a constant force $\vec{F}$ applied at a downward angle $\theta$. The provided graph shows the block's acceleration magnitude $a$ as a linear function of the coefficient of kinetic friction $\mu_k$. The line passes through the points $(0, a_1)$, $(\mu_{k2}, 0)$, and $(\mu_{k3}, -a_1)$, where it can be deduced that $\mu_{k3} = 2\mu_{k2}$.
01K63JDYG45TWF213QGG3FQTTG
Applying Newton's second law in the vertical and horizontal directions:
$$ \Sigma F_y = N - mg - F\sin\theta = 0 \implies N = mg + F\sin\theta $$ $$ \Sigma F_x = F\cos\theta - f_k = ma $$The kinetic friction force is $f_k = \mu_k N$. Substituting $N$ and $f_k$ into the x-equation gives:
$$ F\cos\theta - \mu_k (mg + F\sin\theta) = ma $$Solving for acceleration $a$ as a function of $\mu_k$:
$$ a(\mu_k) = \left(\frac{F\cos\theta}{m}\right) - \mu_k \left(g + \frac{F\sin\theta}{m}\right) $$This is a linear equation of the form $a = A - B\mu_k$. From the graph, we identify the y-intercept and the slope. The y-intercept occurs at $\mu_k=0$, which is given as $a=a_1$.
$$ A = \frac{F\cos\theta}{m} = a_1 $$The slope can be found using the points $(0, a_1)$ and $(\mu_{k2}, 0)$.
$$ \text{Slope} = -B = \frac{0 - a_1}{\mu_{k2} - 0} = -\frac{a_1}{\mu_{k2}} $$ $$ B = g + \frac{F\sin\theta}{m} = \frac{a_1}{\mu_{k2}} $$We now have a system of two equations:
- $\frac{F}{m}\cos\theta = a_1$
- $\frac{F}{m}\sin\theta = \frac{a_1}{\mu_{k2}} - g$
Dividing equation (2) by equation (1) eliminates the term $F/m$:
$$ \frac{\frac{F}{m}\sin\theta}{\frac{F}{m}\cos\theta} = \tan\theta = \frac{\frac{a_1}{\mu_{k2}} - g}{a_1} $$ $$ \tan\theta = \frac{1}{\mu_{k2}} - \frac{g}{a_1} $$