Source: Principles of Physics
Problem Sets:
Problem
Two blocks, with masses $m_A$ and $m_B$, are on a frictionless horizontal surface. They are connected by a string of negligible mass. A force $\vec{F}_A$ acts on block A and a force $\vec{F}_B$ acts on block B. Both forces are directed along the positive x-axis.
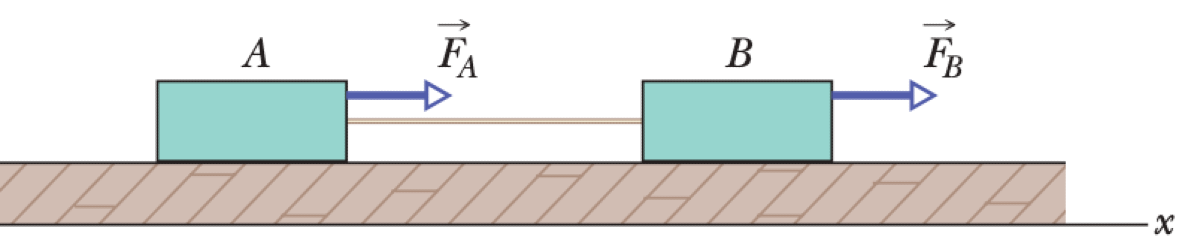
01K63GATYV8PN1QWWRZD6AX1PB
First, consider both blocks as a single system of total mass $M = m_A + m_B$. The net external force is $F_{net} = F_A + F_B$. The acceleration $a$ of the system is given by Newton's second law:
$$a = \frac{F_{net}}{M} = \frac{F_A + F_B}{m_A + m_B}$$Next, apply Newton's second law to an individual block to find the tension, $T$. For block B, the net force is the applied force $F_B$ minus the tension $T$ pulling in the opposite direction.
$$F_B - T = m_B a$$Solving for tension $T$ and substituting the expression for acceleration $a$:
$$T = F_B - m_B a = F_B - m_B \left(\frac{F_A + F_B}{m_A + m_B}\right)$$ $$T = \frac{F_B(m_A + m_B) - m_B(F_A + F_B)}{m_A + m_B}$$ $$T = \frac{m_A F_B + m_B F_B - m_B F_A - m_B F_B}{m_A + m_B}$$Simplifying the expression gives the final result for the tension.