Source: Principles of Physics
Problem
A box of mass $m_1$ rests on a frictionless plane inclined at an angle $\theta_1$. It is connected by a massless cord over a massless, frictionless pulley to a second box of mass $m_2$ on a frictionless plane inclined at an angle $\theta_2$.
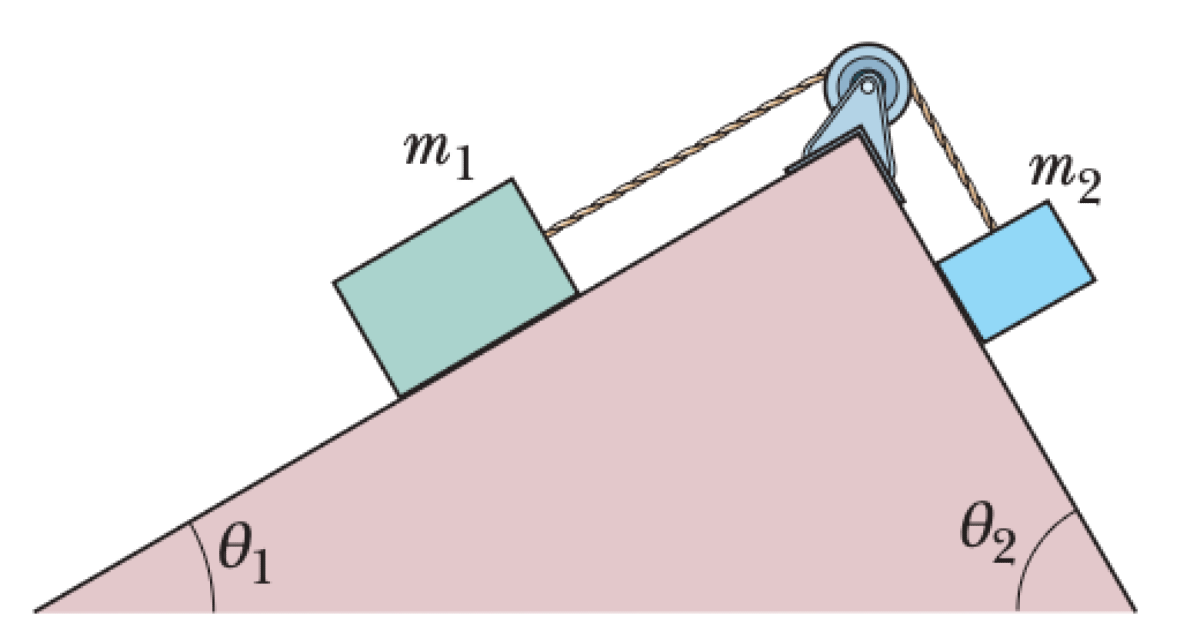
01K63G8384D3WSF4DSMHD12ZDG
[Q1] $T = \frac{m_1 m_2 g (\sin(\theta_1) + \sin(\theta_2))}{m_1 + m_2}$
Let $T$ be the tension in the cord and $a$ be the magnitude of the acceleration of the system. We define the positive direction as $m_1$ accelerating up its incline and $m_2$ accelerating down its incline. Applying Newton's second law to each mass parallel to its incline gives two equations:
For mass $m_1$:
$$T - m_1 g \sin(\theta_1) = m_1 a \quad (1)$$For mass $m_2$:
$$m_2 g \sin(\theta_2) - T = m_2 a \quad (2)$$We can solve this system for $T$ by first isolating $a$ in each equation: From (1): $a = \frac{T}{m_1} - g \sin(\theta_1)$ From (2): $a = g \sin(\theta_2) - \frac{T}{m_2}$
Setting the expressions for $a$ equal to each other eliminates $a$:
$$\frac{T}{m_1} - g \sin(\theta_1) = g \sin(\theta_2) - \frac{T}{m_2}$$Now, we solve for $T$:
$$T \left(\frac{1}{m_1} + \frac{1}{m_2}\right) = g (\sin(\theta_1) + \sin(\theta_2))$$ $$T \left(\frac{m_2 + m_1}{m_1 m_2}\right) = g (\sin(\theta_1) + \sin(\theta_2))$$ $$T = \frac{m_1 m_2 g (\sin(\theta_1) + \sin(\theta_2))}{m_1 + m_2}$$