Source: Principles of Physics
Problem Sets:
Problem
A block of mass $m_1$ on a frictionless horizontal surface is connected by a massless cord over a frictionless, massless pulley to a second block of mass $m_2$ on a frictionless plane tilted at an angle $\theta$. A force $\vec{F}$ is applied to $m_2$, directed up the incline.
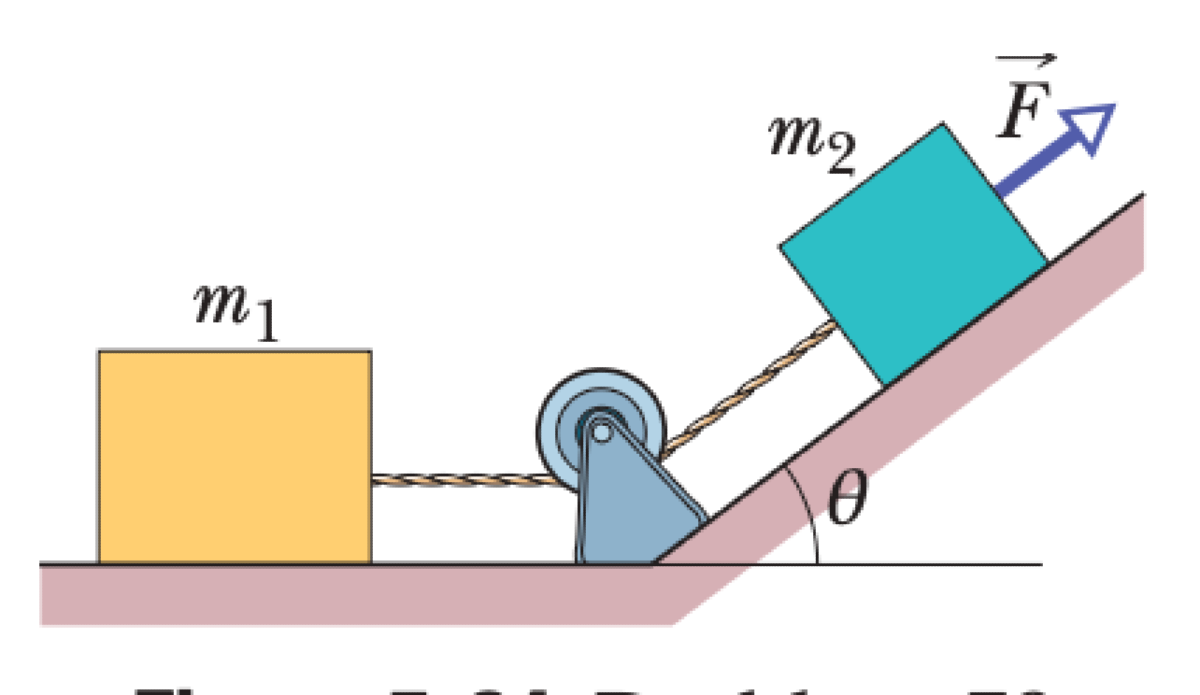
01K63G6KWE91475WAPDEQ3XQWP
Apply Newton's second law to each block, assuming the system accelerates with magnitude $a$.
For block $m_1$ on the horizontal surface, the net force is the tension $T$:
$$T = m_1 a$$For block $m_2$ along the incline, the net force is the sum of the applied force, tension, and the component of gravity parallel to the incline:
$$F - T - m_2 g \sin\theta = m_2 a$$To find the tension, we can solve the system of two equations. From the first equation, express acceleration as $a = T/m_1$. Substitute this into the second equation to eliminate $a$:
$$F - T - m_2 g \sin\theta = m_2 \left(\frac{T}{m_1}\right)$$Now, solve algebraically for $T$:
$$m_1 F - m_1 T - m_1 m_2 g \sin\theta = m_2 T$$ $$m_1 F - m_1 m_2 g \sin\theta = T(m_1 + m_2)$$ $$T = \frac{m_1(F - m_2 g \sin\theta)}{m_1 + m_2}$$