Source: Principles of Physics
Problem
A person and chair of combined mass $M$ are suspended by a massless rope over a massless, frictionless pulley. The system is to rise with an upward acceleration $a$. The rope's free end can be pulled either by the person in the chair or by a co-worker on the ground.
- Find the force magnitude, $F_{man}$, with which the person must pull.
- Find the force magnitude, $F_{co}$, with which a co-worker must pull.
- Find the force magnitude on the ceiling, $F_{ceil,1}$, when the person pulls.
- Find the force magnitude on the ceiling, $F_{ceil,2}$, when the co-worker pulls.
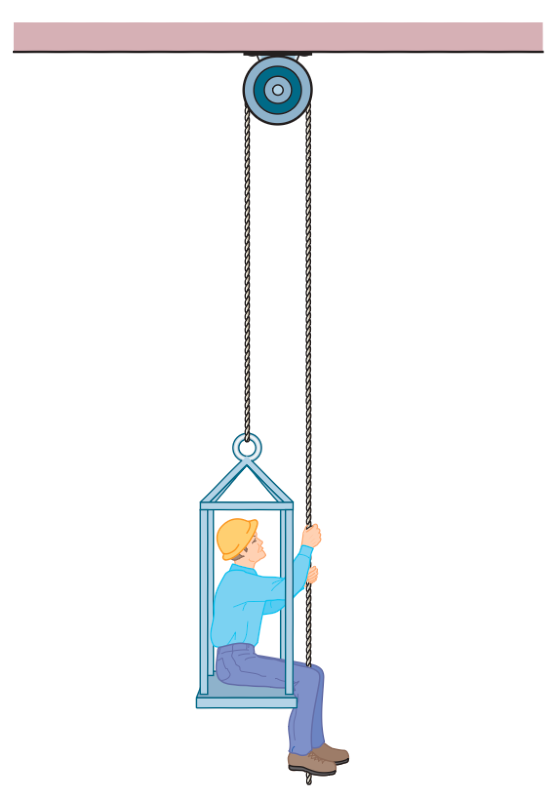
01K62AZPD4H098831SR9KYB7GE
[Q1] $F_{man} = \frac{1}{2} M(g+a)$ [Q2] $F_{co} = M(g+a)$ [Q3] $F_{ceil,1} = M(g+a)$ [Q4] $F_{ceil,2} = 2M(g+a)$
Let $T$ be the tension in the rope. The net force on the person-chair system of mass $M$ is given by Newton's second law, $\sum F_y = F_{up} - Mg = Ma$.
Case 1: The person pulls the rope. The system is supported by two upward forces from the rope: one on the chair and one on the person's hands. Since the person's pulling force equals the tension, $F_{man} = T$, the total upward force is $F_{up} = T + T = 2T$. Applying Newton's second law:
$$2T - Mg = Ma \implies T = \frac{M(g+a)}{2}$$The person's pulling force is $F_{man} = T$. The force on the ceiling is the total downward pull on the pulley from both rope segments, so $F_{ceil,1} = 2T$.
Case 2: A co-worker pulls the rope. The system is now supported by only one rope segment. The co-worker's pull creates the tension, $F_{co} = T$. The upward force on the system is $F_{up} = T$. Applying Newton's second law:
$$T - Mg = Ma \implies T = M(g+a)$$The co-worker's pulling force is $F_{co} = T$. The force on the ceiling is again the sum of tensions in both rope segments, $F_{ceil,2} = 2T$.