Source: Principles of Physics
Problem
A chain consists of $N$ links, each of mass $m$. It is lifted vertically with a constant upward acceleration of magnitude $a$. The links are numbered 1 to $N$ from bottom to top. Let $g$ be the acceleration due to gravity.
- Find the magnitude of the force $F_{k+1, k}$ on link $k$ from link $k+1$, for any link $k$ where $1 \le k < N$.
- Find the magnitude of the external force $F$ on the top link ($N$) lifting the entire chain.
- Find the magnitude of the net force $F_{net}$ on any single link.
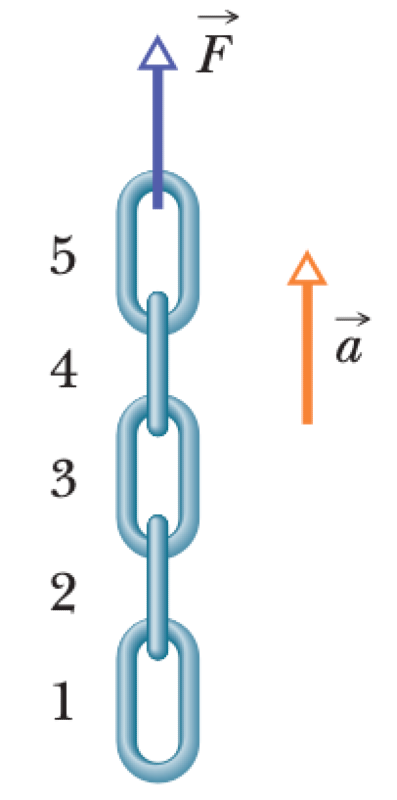
01K62AYYFMBVSBMPW25CES2RF8
[Q1] $F_{k+1, k} = km(a+g)$ [Q2] $F = Nm(a+g)$ [Q3] $F_{net} = ma$
Let the upward direction be positive. We apply Newton's second law, $\sum F = Ma_{sys}$, to different parts of the chain.
For the net force on a single link [Q3]: Each link has mass $m$ and acceleration $a$.
$$F_{net} = ma$$For the force between links [Q1]: Consider a system consisting of the bottom $k$ links. The total mass of this system is $M_k = km$. The external forces are the upward force from link $k+1$ ($F_{k+1, k}$) and the total downward weight of the system ($W_k = M_k g = kmg$). Applying Newton's second law to this system:
$$F_{k+1, k} - W_k = M_k a$$ $$F_{k+1, k} - kmg = (km)a$$ $$F_{k+1, k} = km(a+g)$$For the external lifting force [Q2]: This force must lift and accelerate the entire chain of $N$ links. We can use the previous result by considering the system of all $N$ links (i.e., setting $k=N$). The total mass is $M_{total} = Nm$.
$$F = Nm(a+g)$$