Source: Principles of Physics
Problem
A block of mass $m$ is pulled along a horizontal frictionless floor by a cord that exerts a force of magnitude $F$ at an angle $\theta$ above the horizontal.
- What is the magnitude of the block's acceleration?
- What is the magnitude of the force $F$ just before the block is lifted completely off the floor?
- What is the magnitude of the block's acceleration just before it is lifted completely off the floor?
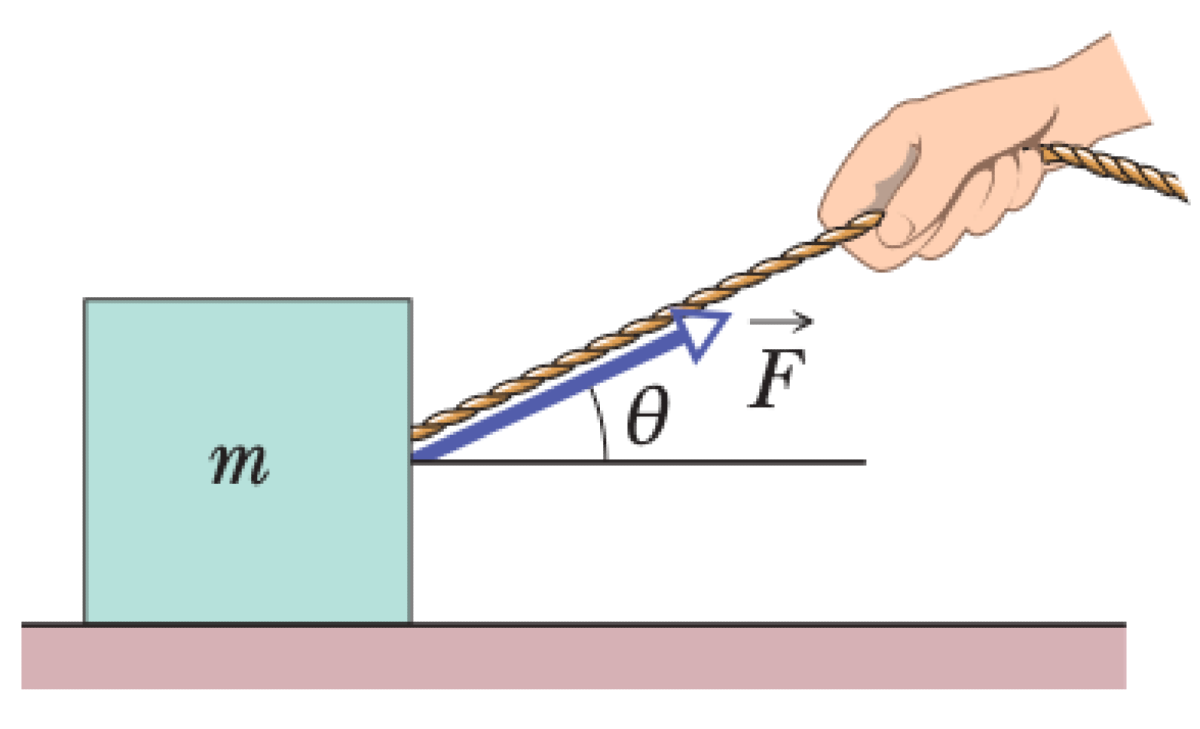
01K62AY77BNBNFW6Y3CAHYVGAW
[Q1] $a = \frac{F \cos\theta}{m}$ [Q2] $F = \frac{mg}{\sin\theta}$ [Q3] $a = g \cot\theta$
We apply Newton's second law by analyzing the horizontal and vertical components of the forces. Let the acceleration be $a$, the normal force be $N$, and gravitational acceleration be $g$.
[Q1] The only horizontal force is the x-component of the applied force $F$.
$$ \sum F_x = F \cos\theta = ma $$Solving for the acceleration $a$:
$$ a = \frac{F \cos\theta}{m} $$[Q2] The block lifts off the floor when the normal force $N$ becomes zero. The vertical forces are the upward normal force $N$, the upward vertical component of $F$, and the downward force of gravity $mg$.
$$ \sum F_y = N + F \sin\theta - mg = 0 $$Setting $N=0$ for liftoff:
$$ F \sin\theta - mg = 0 $$Solving for the liftoff force $F$:
$$ F = \frac{mg}{\sin\theta} $$[Q3] To find the acceleration just before liftoff, we substitute the liftoff force from [Q2] into the acceleration equation from [Q1].
$$ a = \frac{1}{m} \left( \frac{mg}{\sin\theta} \right) \cos\theta $$Simplifying the expression gives the acceleration at liftoff:
$$ a = g \frac{\cos\theta}{\sin\theta} = g \cot\theta $$