Source: Principles of Physics
Problem
Two elevator cabs, A and B, with masses $m_A$ and $m_B$ respectively, are connected by a cable. A box of mass $m_{box}$ rests on the floor of cab A. The entire system is moved by another cable attached to cab A. The tension in the cable connecting the two cabs is $T_{AB}$.
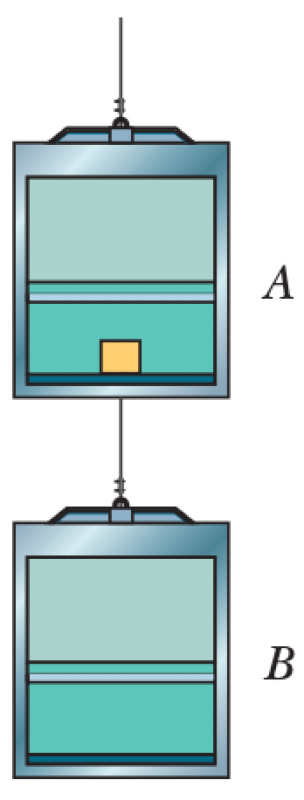
01K62AXBWQ0137H3ESSZ6V22K6
First, determine the acceleration of the system, $a$, by applying Newton's second law to cab B. The forces on cab B are the upward tension $T_{AB}$ and the downward gravitational force $m_B g$.
$$T_{AB} - m_B g = m_B a$$ $$a = \frac{T_{AB} - m_B g}{m_B}$$Next, apply Newton's second law to the box, which shares the same acceleration $a$. The forces on the box are the upward normal force $F_N$ and the downward gravitational force $m_{box} g$.
$$F_N - m_{box} g = m_{box} a$$ $$F_N = m_{box}(g + a)$$Substitute the expression for acceleration $a$ into the equation for the normal force $F_N$.
$$F_N = m_{box} \left( g + \frac{T_{AB} - m_B g}{m_B} \right)$$ $$F_N = m_{box} \left( \frac{m_B g + T_{AB} - m_B g}{m_B} \right)$$ $$F_N = m_{box} \left( \frac{T_{AB}}{m_B} \right)$$