Source: Principles of Physics
Problem
A constant horizontal force $\vec{F}_a$ is applied to a system of two blocks, A and B, with masses $m_A$ and $m_B$ and total mass $M = m_A + m_B$. Case 1: When the force is applied to block A, the magnitude of the contact force between the blocks is $F_1$. Case 2: When the same force is applied to block B, the magnitude of the contact force is $F_2$.
- What is the magnitude of the system's acceleration, $a$?
- What is the magnitude of the applied force, $F_a$?
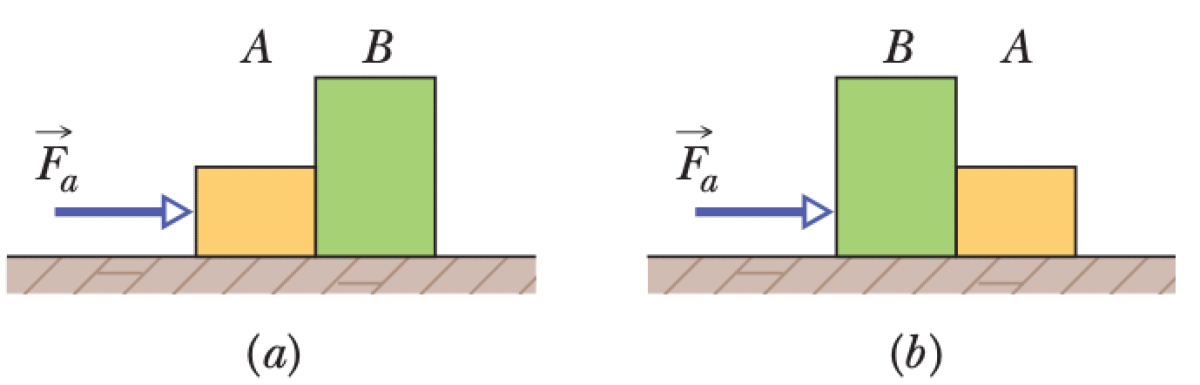
01K62AS6CJX2XQJF5P7MB0G0WJ
[Q1] $a = \frac{F_1 + F_2}{M}$ [Q2] $F_a = F_1 + F_2$
Let $a$ be the acceleration of the system. Since the total mass $M$ and the net applied force $F_a$ are the same in both cases, the acceleration $a$ is also the same.
In Case 1 (force on A), the contact force $F_1$ is the only horizontal force acting on block B. Applying Newton's second law to block B:
$$F_1 = m_B a$$In Case 2 (force on B), the contact force $F_2$ is the only horizontal force acting on block A. Applying Newton's second law to block A:
$$F_2 = m_A a$$The total applied force $F_a$ accelerates the total mass $M$:
$$F_a = M a = (m_A + m_B)a$$Substituting the expressions for $m_A a$ and $m_B a$:
$$F_a = F_2 + F_1$$The acceleration $a$ can then be found from the total force and total mass:
$$a = \frac{F_a}{M} = \frac{F_1 + F_2}{M}$$