Source: Principles of Physics
Problem
A horse pulls a barge of mass $m$ with a force of magnitude $F_H$ at an angle $\theta$ relative to the direction of motion. The barge moves along the positive x-axis with a constant acceleration of magnitude $a$.
- What is the magnitude of the force on the barge from the water, $F_W$?
- What is the direction $\phi$ (relative to the positive x-axis) of the force on the barge from the water?
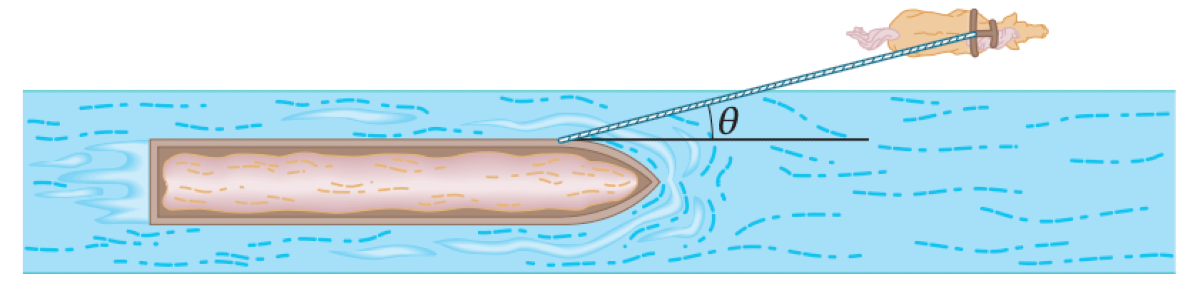
01K62DMEHHDS39PP2QP1YS5V5Z
[Q1] $F_W = \sqrt{(ma)^2 + F_H^2 - 2maF_H\cos\theta}$ [Q2] $\phi = \arctan\left(\frac{-F_H \sin\theta}{ma - F_H \cos\theta}\right)$
Let the force from the horse be $\vec{F}_H$ and the force from the water be $\vec{F}_W$. The barge's acceleration is $\vec{a} = a\hat{i}$. We apply Newton's Second Law, $\sum \vec{F} = m\vec{a}$.
$$ \vec{F}_H + \vec{F}_W = m\vec{a} $$Solving for the force from the water gives:
$$ \vec{F}_W = m\vec{a} - \vec{F}_H $$We can find the components of $\vec{F}_W$ by resolving the vectors into x and y components.
$$ \vec{F}_H = (F_H \cos\theta)\hat{i} + (F_H \sin\theta)\hat{j} $$ $$ m\vec{a} = (ma)\hat{i} $$The components of $\vec{F}_W = F_{W,x}\hat{i} + F_{W,y}\hat{j}$ are therefore:
$$ F_{W,x} = ma - F_H \cos\theta $$ $$ F_{W,y} = 0 - F_H \sin\theta = -F_H \sin\theta $$The magnitude $F_W$ is found using the Pythagorean theorem:
$$ F_W = \sqrt{F_{W,x}^2 + F_{W,y}^2} = \sqrt{(ma - F_H \cos\theta)^2 + (-F_H \sin\theta)^2} $$ $$ F_W = \sqrt{m^2a^2 - 2maF_H\cos\theta + F_H^2\cos^2\theta + F_H^2\sin^2\theta} $$ $$ F_W = \sqrt{(ma)^2 + F_H^2 - 2maF_H\cos\theta} $$The direction $\phi$ is found from the ratio of the components:
$$ \tan\phi = \frac{F_{W,y}}{F_{W,x}} = \frac{-F_H \sin\theta}{ma - F_H \cos\theta} $$