Source: Principles of Physics
Problem
Four objects with masses $m_1, m_2, m_3,$ and $m_4$ are connected by three massless cords and pulled along a frictionless horizontal surface. The tension in the cord pulling the entire system is $T_4$, and the tension in the cord between objects 2 and 3 is $T_2$. The masses $m_1, m_3, m_4$, and the tensions $T_2, T_4$ are known.
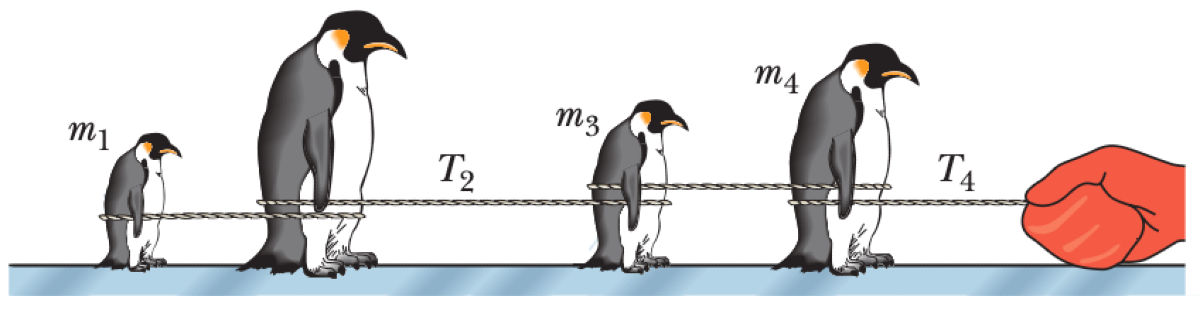
01K62APFJXSQB00AM05H00X1DN
Since the objects are connected and move together, they share a common acceleration, $a$. We apply Newton's second law, $\Sigma F=ma$, to two different subsystems.
Consider the subsystem of masses $m_1$ and $m_2$. The net force is the tension $T_2$.
$$T_2 = (m_1 + m_2)a$$Consider the subsystem of masses $m_3$ and $m_4$. The net force is the difference between the forward tension $T_4$ and the backward tension $T_2$.
$$T_4 - T_2 = (m_3 + m_4)a$$To eliminate the acceleration $a$, we can solve for $a$ in each equation and set them equal, or simply divide the two equations:
$$\frac{m_1 + m_2}{m_3 + m_4} = \frac{T_2}{T_4 - T_2}$$Now, we solve for the unknown mass $m_2$:
$$m_1 + m_2 = (m_3 + m_4) \frac{T_2}{T_4 - T_2}$$ $$m_2 = (m_3 + m_4) \frac{T_2}{T_4 - T_2} - m_1$$