Source: Principles of Physics
Problem
Three blocks with masses $m_A$, $m_B$, and $m_C$ are connected by massless cords as shown. One cord passes over a massless, frictionless pulley. The block with mass $m_A$ rests on a frictionless horizontal surface. The system is released from rest.
- What is the tension, $T_{BC}$, in the cord connecting blocks B and C?
- How far, $d$, does block A move in a time $t$?
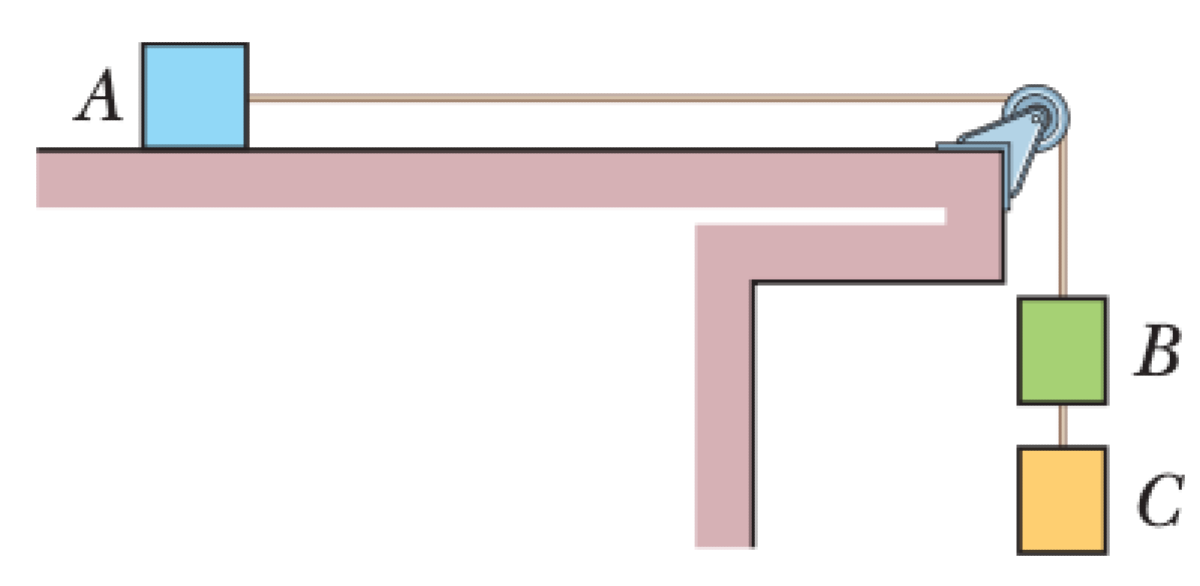
01K62ANN63TSDHWDNDCYK7R2DB
[Q1] $T_{BC} = \frac{m_A m_C g}{m_A + m_B + m_C}$ [Q2] $d = \frac{(m_B + m_C) g t^2}{2(m_A + m_B + m_C)}$
We consider all three blocks as a single system with total mass $M = m_A + m_B + m_C$. The net external force driving the system is the gravitational force on the hanging blocks, $F_{net} = (m_B + m_C)g$.
Using Newton's second law, $F_{net} = Ma$, we find the acceleration $a$ of the system:
$$ (m_B + m_C)g = (m_A + m_B + m_C)a $$ $$ a = \frac{(m_B + m_C)g}{m_A + m_B + m_C} $$[Q1] To find the tension $T_{BC}$, we apply Newton's second law to block C alone. Taking the downward direction as positive:
$$ \Sigma F_C = m_C g - T_{BC} = m_C a $$ $$ T_{BC} = m_C(g - a) $$Substituting the expression for $a$:
$$ T_{BC} = m_C \left( g - \frac{(m_B + m_C)g}{m_A + m_B + m_C} \right) = m_C g \left( \frac{(m_A + m_B + m_C) - (m_B + m_C)}{m_A + m_B + m_C} \right) $$ $$ T_{BC} = \frac{m_A m_C g}{m_A + m_B + m_C} $$[Q2] Since the system starts from rest ($v_0 = 0$) and has constant acceleration $a$, we use the kinematic equation for displacement:
$$ d = v_0 t + \frac{1}{2} a t^2 = \frac{1}{2} a t^2 $$Substituting the expression for $a$:
$$ d = \frac{1}{2} \left( \frac{(m_B + m_C)g}{m_A + m_B + m_C} \right) t^2 $$