Source: Principles of Physics
Problem Sets:
Problem
Three blocks with masses $m_A$, $m_B$, and $m_C$ are connected by massless cords that loop over frictionless pulleys as shown. Block B lies on a frictionless table. The blocks are released from rest. Assume $m_C > m_A$.
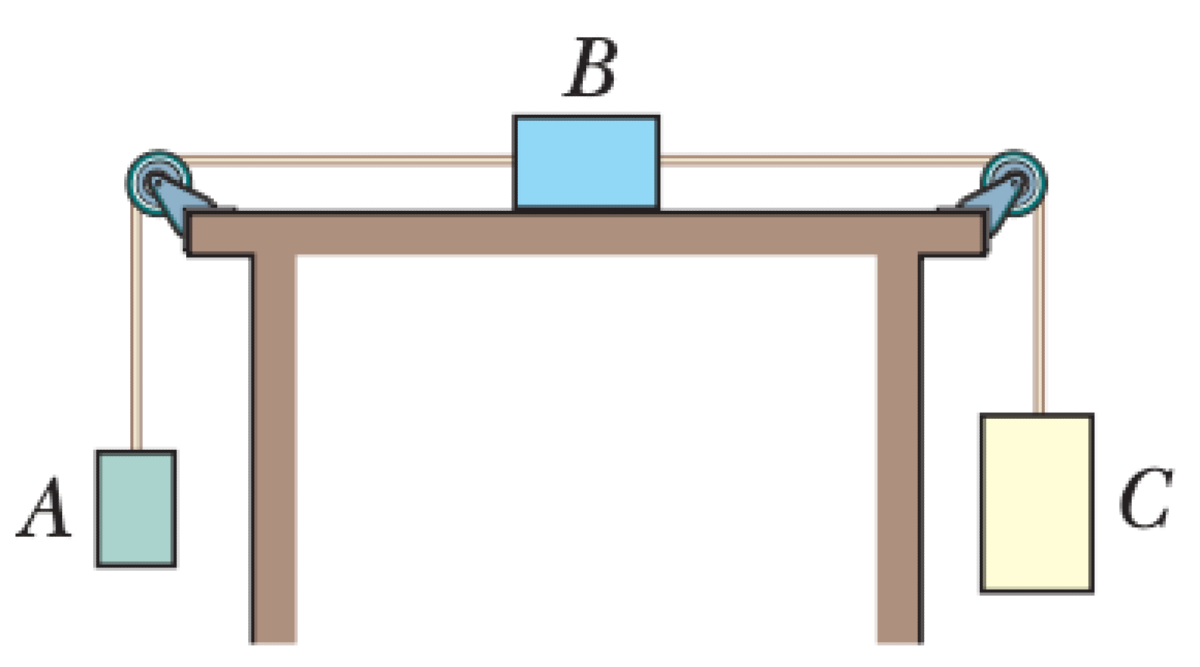
01K62AMF81FK14K0TMYWJ48HP0
Consider the three blocks as a single system. The total mass is $M = m_A + m_B + m_C$. The net external force causing acceleration is the difference between the weights of the hanging blocks, $F_{net} = m_C g - m_A g = (m_C - m_A)g$.
Applying Newton's second law to the system, $F_{net} = Ma$:
$$(m_C - m_A)g = (m_A + m_B + m_C)a$$The acceleration of the system is:
$$a = \frac{(m_C - m_A)g}{m_A + m_B + m_C}$$To find the tension in the right cord, $T_{BC}$, apply Newton's second law to block C. The net force on block C is $m_C g - T_{BC}$, as it accelerates downward.
$$m_C g - T_{BC} = m_C a$$Solving for $T_{BC}$ and substituting the expression for $a$:
$$T_{BC} = m_C(g - a) = m_C \left( g - \frac{(m_C - m_A)g}{m_A + m_B + m_C} \right)$$ $$T_{BC} = m_C g \left( 1 - \frac{m_C - m_A}{m_A + m_B + m_C} \right)$$ $$T_{BC} = m_C g \left( \frac{(m_A + m_B + m_C) - (m_C - m_A)}{m_A + m_B + m_C} \right)$$ $$T_{BC} = m_C g \left( \frac{2m_A + m_B}{m_A + m_B + m_C} \right)$$