Source: Principles of Physics
Problem Sets:
Problem
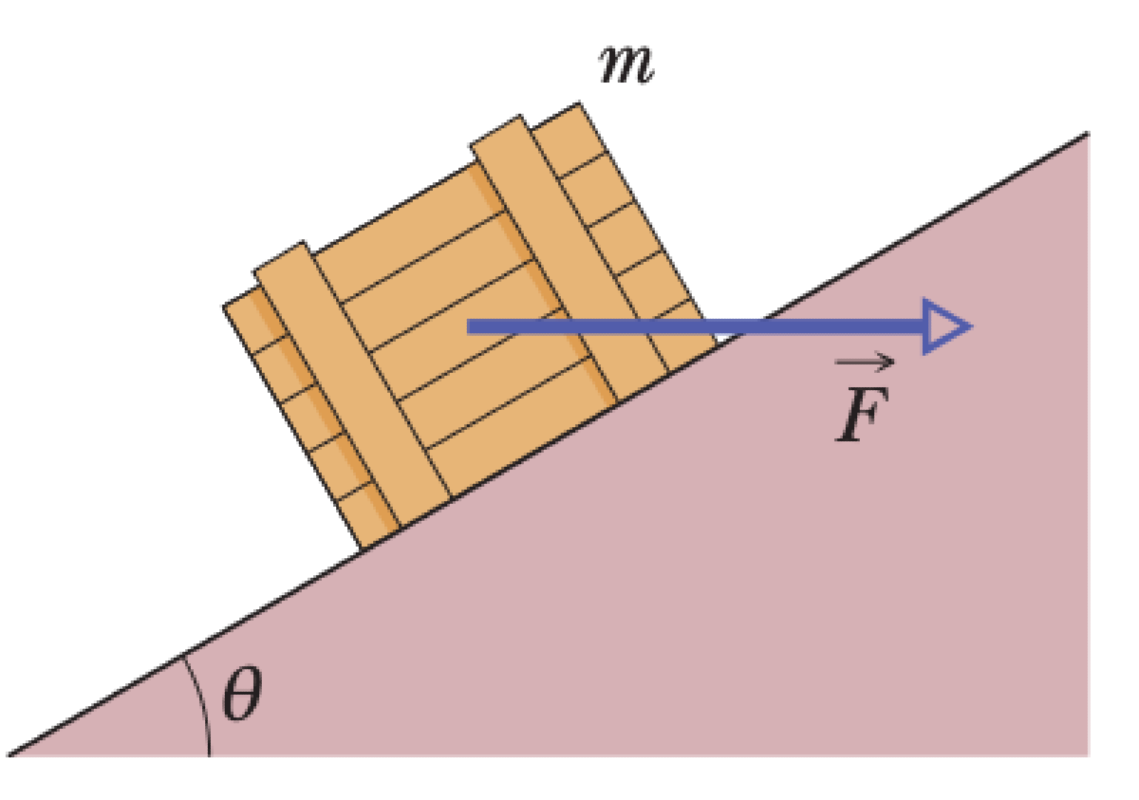
A crate of mass $m$ is pushed at a constant speed up a frictionless ramp inclined at an angle $\theta$ to the horizontal. The crate is pushed by a horizontal force $\vec{F}$.
- What is the magnitude of the force $\vec{F}$?
- What is the magnitude of the normal force $N$ exerted on the crate by the ramp?
01K62AKJF590EEB0DQH1VY3STH
[Q1] $F = mg \tan\theta$ [Q2] $N = \frac{mg}{\cos\theta}$
Since the crate moves at a constant speed, its acceleration is zero, and the net force is zero ($\sum \vec{F} = 0$). We resolve the forces into components parallel ($x$) and perpendicular ($y$) to the ramp.
The forces acting on the crate are the gravitational force ($mg$), the horizontal force ($F$), and the normal force ($N$).
Sum of forces parallel to the ramp:
$$ \sum F_x = F \cos\theta - mg \sin\theta = 0 $$Solving for $F$ gives the magnitude of the applied horizontal force.
$$ F = mg \frac{\sin\theta}{\cos\theta} = mg \tan\theta $$Sum of forces perpendicular to the ramp:
$$ \sum F_y = N - mg \cos\theta - F \sin\theta = 0 $$ $$ N = mg \cos\theta + F \sin\theta $$Substitute the expression for $F$:
$$ N = mg \cos\theta + (mg \tan\theta) \sin\theta = mg \left( \cos\theta + \frac{\sin^2\theta}{\cos\theta} \right) $$Using the common denominator $\cos\theta$ and the identity $\cos^2\theta + \sin^2\theta = 1$:
$$ N = mg \left( \frac{\cos^2\theta + \sin^2\theta}{\cos\theta} \right) = \frac{mg}{\cos\theta} $$