Source: Principles of Physics
Problem Sets:
Problem
A block of mass $m_1$ is on a frictionless plane inclined at an angle $\theta$. It is connected by a massless cord over a massless, frictionless pulley to a second, hanging block of mass $m_2$.
- What is the magnitude of the acceleration of each block?
- What is the direction of the acceleration of the hanging block?
- What is the tension in the cord?
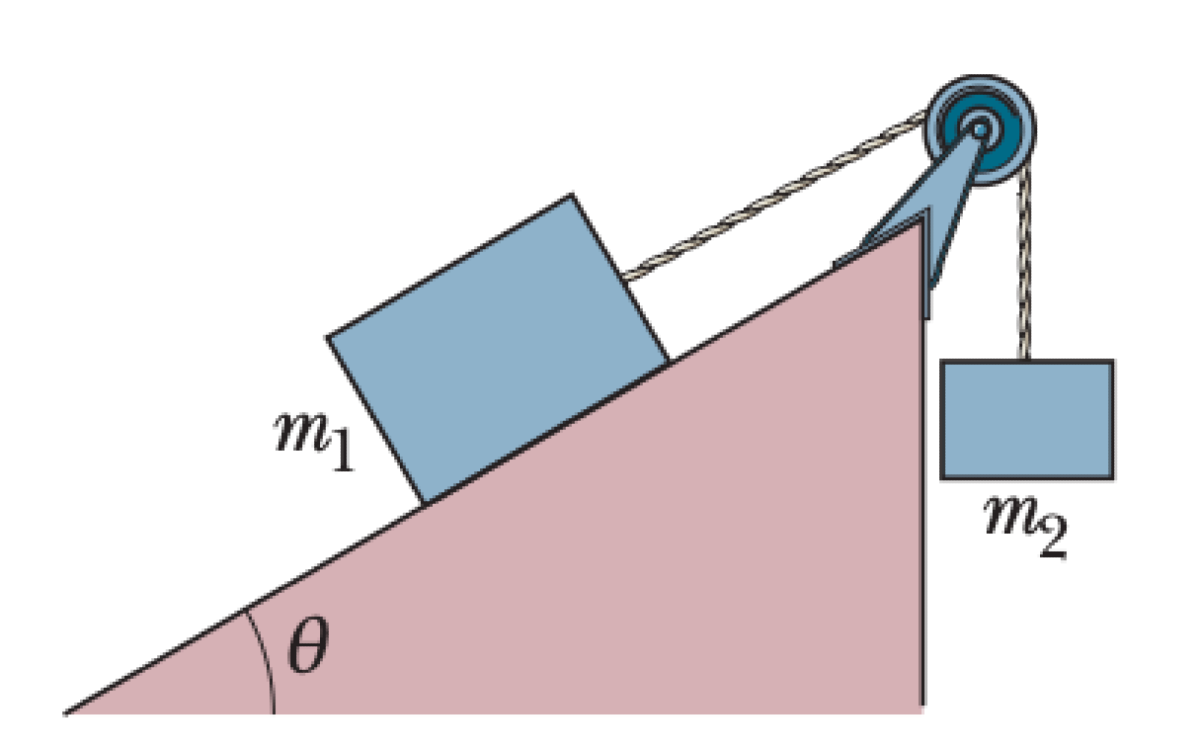
01K62AJ4H9RBJEFS2W66QC1P66
[Q1] $a = \frac{g |m_2 - m_1 \sin\theta|}{m_1 + m_2}$ [Q2] The hanging block accelerates downward if $m_2 > m_1 \sin\theta$ and upward if $m_2 < m_1 \sin\theta$. [Q3] $T = \frac{m_1 m_2 g(1 + \sin\theta)}{m_1 + m_2}$
We apply Newton's second law to each block. Let's define the positive direction as $m_1$ accelerating up the incline and $m_2$ accelerating downward. The magnitude of acceleration, $a$, and the tension, $T$, are the same for both blocks.
For block $m_1$ on the incline, the net force along the incline is:
$$T - m_1g \sin\theta = m_1a \quad (1)$$For the hanging block $m_2$, the net force is:
$$m_2g - T = m_2a \quad (2)$$To find the acceleration, we add equations (1) and (2) to eliminate $T$:
$$(T - m_1g \sin\theta) + (m_2g - T) = m_1a + m_2a$$ $$m_2g - m_1g \sin\theta = (m_1 + m_2)a$$Solving for $a$ gives the acceleration:
$$a = \frac{g(m_2 - m_1 \sin\theta)}{m_1 + m_2}$$The direction of motion depends on the sign of the numerator. If $m_2 > m_1 \sin\theta$, $a$ is positive and $m_2$ accelerates downward. If $m_2 < m_1 \sin\theta$, $a$ is negative and $m_2$ accelerates upward.
To find the tension, substitute the expression for $a$ back into equation (2):
$$T = m_2(g - a) = m_2\left(g - \frac{g(m_2 - m_1 \sin\theta)}{m_1 + m_2}\right)$$ $$T = m_2g \left(1 - \frac{m_2 - m_1 \sin\theta}{m_1 + m_2}\right) = m_2g \left(\frac{(m_1 + m_2) - (m_2 - m_1 \sin\theta)}{m_1 + m_2}\right)$$ $$T = \frac{m_1 m_2 g(1 + \sin\theta)}{m_1 + m_2}$$