Source: Principles of Physics
Problem
Three connected blocks with masses $m_1$, $m_2$, and $m_3$ are pulled to the right on a horizontal frictionless table by a force of magnitude $T_3$.
- Find an expression for the magnitude of the system's acceleration, $a$.
- Find an expression for the tension $T_1$.
- Find an expression for the tension $T_2$.
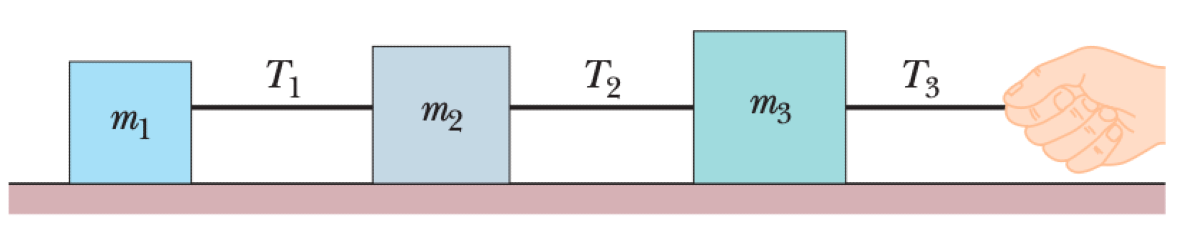
01K62AH1104XWX1WKPWPJ5F5SV
[Q1] $a = \frac{T_3}{m_1 + m_2 + m_3}$ [Q2] $T_1 = \frac{m_1 T_3}{m_1 + m_2 + m_3}$ [Q3] $T_2 = \frac{(m_1 + m_2) T_3}{m_1 + m_2 + m_3}$
We treat all three blocks as a single system of total mass $M = m_1 + m_2 + m_3$. The net external force on the system is $T_3$. Applying Newton's second law to the entire system:
$$T_3 = Ma = (m_1 + m_2 + m_3)a$$Solving for the acceleration $a$ gives the answer to [Q1].
To find the tension $T_1$, we apply Newton's second law to block $m_1$. The only horizontal force acting on it is $T_1$.
$$T_1 = m_1 a$$Substituting the expression for $a$ yields the solution for [Q2].
To find the tension $T_2$, we apply Newton's second law to the system consisting of blocks $m_1$ and $m_2$. The net force is $T_2$ and the total mass is $(m_1 + m_2)$.
$$T_2 = (m_1 + m_2)a$$Substituting the expression for $a$ yields the solution for [Q3].