Source: High school physics (Chinese)
Problem
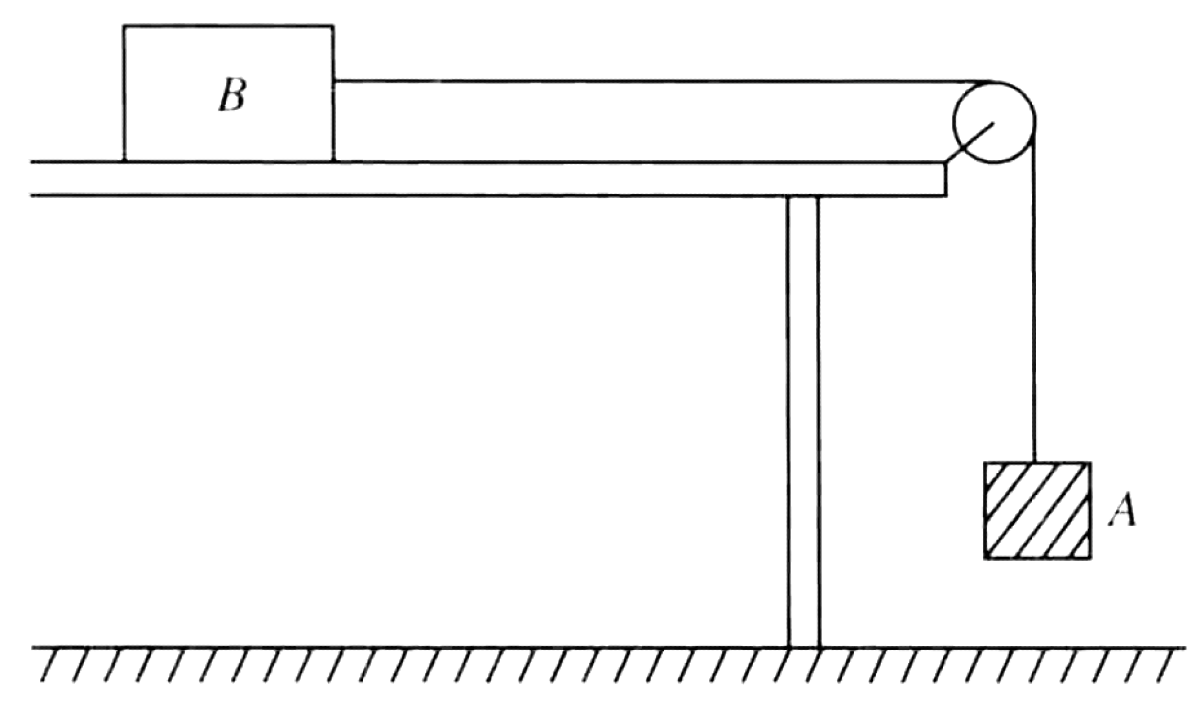
Two objects, A and B, with masses $m_A$ and $m_B$ respectively, are connected by a massless string over a frictionless, massless pulley as shown in the diagram. Object B rests on a horizontal table with a coefficient of kinetic friction $\mu$. The system is initially held at rest with the string taut and is then released.
- Assuming $m_A > \mu m_B$, find the acceleration of the system and the tension in the string.
- What are the acceleration and tension if $m_A \leq \mu m_B$?
01K5Z1F6YDFCR4CFKXH0R4EPT0
[Q1] For $m_A > \mu m_B$: The acceleration of the system is:
$$a = \frac{m_A - \mu m_B}{m_A + m_B}g$$The tension in the string is:
$$T = \frac{m_A m_B g(1 + \mu)}{m_A + m_B}$$[Q2] For $m_A \leq \mu m_B$: The system remains at rest. The acceleration of the system is:
$$a = 0$$The tension in the string is:
$$T = m_A g$$[Q1] Case: $m_A > \mu m_B$ (System Accelerates)
The condition $m_A g > \mu m_B g$ indicates that the gravitational force on mass A is greater than the maximum friction force on mass B, so the system will accelerate. Let $a$ be the magnitude of the acceleration of both masses and $T$ be the tension in the string.
-
Equations of Motion: We apply Newton's second law to each object. Assume A accelerates downwards and B accelerates to the right.
-
For mass A (vertical motion): The net force is the weight minus the tension.
$$m_A g - T = m_A a \quad (1)$$ -
For mass B (horizontal motion): The net force is the tension minus the kinetic friction force, $f_k$. The normal force on B is $N = m_B g$, so the kinetic friction is $f_k = \mu N = \mu m_B g$.
$$T - \mu m_B g = m_B a \quad (2)$$
-
-
Solve for Acceleration ($a$): Add equations (1) and (2) to eliminate the tension $T$.
$$(m_A g - T) + (T - \mu m_B g) = m_A a + m_B a$$ $$g(m_A - \mu m_B) = (m_A + m_B)a$$ $$a = \frac{m_A - \mu m_B}{m_A + m_B}g$$ -
Solve for Tension ($T$): Substitute the expression for $a$ back into equation (2).
$$T = m_B a + \mu m_B g$$ $$T = m_B \left( \frac{m_A - \mu m_B}{m_A + m_B}g \right) + \mu m_B g$$ $$T = \frac{m_A m_B g - \mu m_B^2 g + \mu m_B g(m_A + m_B)}{m_A + m_B}$$ $$T = \frac{m_A m_B g - \mu m_B^2 g + \mu m_A m_B g + \mu m_B^2 g}{m_A + m_B}$$ $$T = \frac{m_A m_B g(1 + \mu)}{m_A + m_B}$$
[Q2] Case: $m_A \leq \mu m_B$ (System at Rest)
-
Condition for Static Equilibrium: The system is initially at rest. The driving force attempting to cause motion is the weight of A, $W_A = m_A g$. The maximum static friction force that resists the motion is $f_{s,max} = \mu_s N = \mu_s m_B g$. Assuming the coefficient of static friction $\mu_s$ is at least as large as the given kinetic friction coefficient $\mu$, the condition for the system to remain at rest is $W_A \leq f_{s,max}$. The problem condition is $m_A \leq \mu m_B$, which is equivalent to $m_A g \leq \mu m_B g$. This means the driving force is less than or equal to the maximum available friction force. Therefore, the system remains in static equilibrium.
-
Acceleration and Tension:
- Since the system does not move, its acceleration is zero. $$a = 0$$
- With $a=0$, we analyze the forces on mass A in equilibrium. $$m_A g - T = m_A(0) = 0$$ $$T = m_A g$$