Source: High school physics (Chinese)
Problem
As shown in Figure, a smooth cylinder of mass $m$ is placed in a V-shaped groove of mass $M$. The cross-section of the groove is symmetric, with each side making an angle $\alpha$ with the horizontal, where $\alpha < 45^\circ$. The groove rests on a frictionless horizontal surface. The groove is connected by a thin, massless string that passes over a frictionless, massless pulley to a hanging weight of mass $m_1$. The system is released from rest. When $m_1$ is sufficiently large, the cylinder can leave the groove.
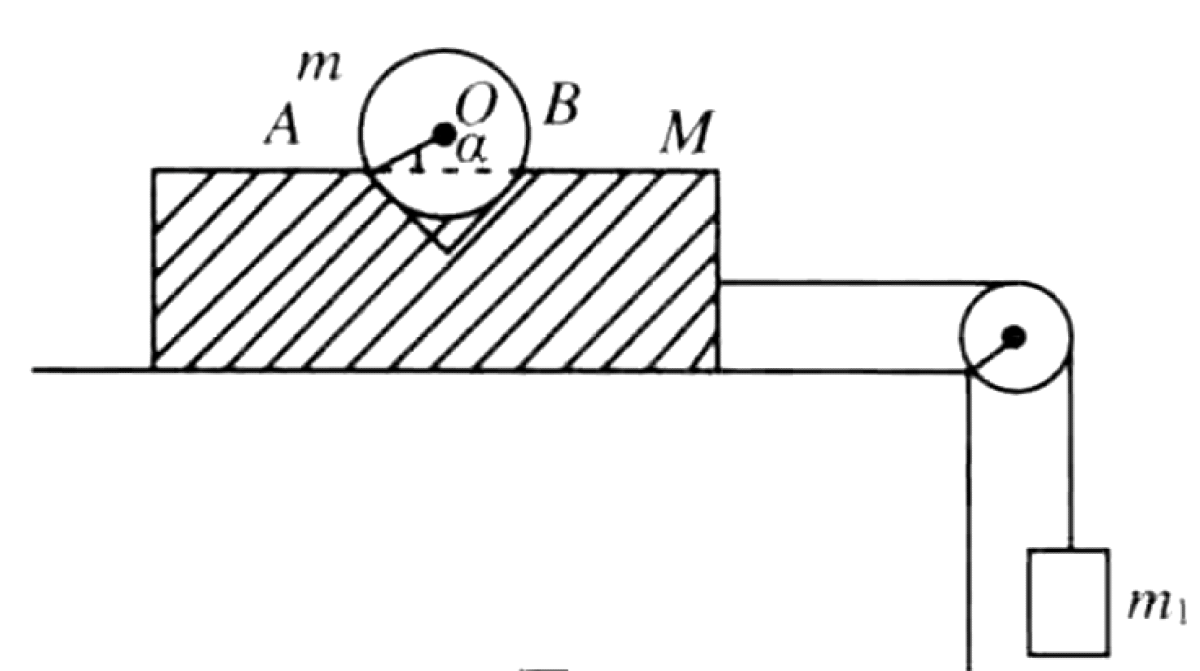
01K5Z1HXXZ3F5SC3J55186HCQM
To ensure the cylinder does not leave the V-shaped groove, the mass $m_1$ must satisfy the condition:
$$m_1 \le \frac{(M+m)\tan\alpha}{1 - \tan\alpha}$$To determine the condition for the cylinder not to leave the V-groove, we must find the maximum possible acceleration of the system before the cylinder lifts off.
1. Dynamics of the Cylinder and Condition for Not Leaving the Groove
First, consider the forces acting on the cylinder of mass $m$. Let the system accelerate horizontally to the right with acceleration $a$. The cylinder also moves with this acceleration $a$, and for it to not leave the groove, its vertical acceleration must be zero. The forces on the cylinder are its weight $mg$ acting downwards, and the normal forces from the two sides of the groove, $N_L$ (left) and $N_R$ (right). By symmetry, both normal forces make an angle $\alpha$ with the vertical.
Applying Newton's second law in the horizontal (x) and vertical (y) directions:
$$ \sum F_x = N_L \sin\alpha - N_R \sin\alpha = ma \quad (1) $$ $$ \sum F_y = N_L \cos\alpha + N_R \cos\alpha - mg = 0 \quad (2) $$From equation (2), we find the sum of the normal forces:
$$ N_L + N_R = \frac{mg}{\cos\alpha} $$From equation (1), we find the difference:
$$ N_L - N_R = \frac{ma}{\sin\alpha} $$Solving for $N_L$ and $N_R$:
$$ N_L = \frac{m}{2} \left(\frac{g}{\cos\alpha} + \frac{a}{\sin\alpha}\right) $$ $$ N_R = \frac{m}{2} \left(\frac{g}{\cos\alpha} - \frac{a}{\sin\alpha}\right) $$For the cylinder to remain in the groove, it must stay in contact with both surfaces, which means both normal forces must be non-negative ($N_L \ge 0$ and $N_R \ge 0$). As acceleration $a$ increases, $N_L$ increases while $N_R$ decreases. The cylinder will lose contact with the right surface first. The limiting condition is thus $N_R \ge 0$.
$$ \frac{m}{2} \left(\frac{g}{\cos\alpha} - \frac{a}{\sin\alpha}\right) \ge 0 $$ $$ \frac{g}{\cos\alpha} \ge \frac{a}{\sin\alpha} $$This gives the maximum acceleration allowed for the cylinder to stay in the groove:
$$ a \le g \tan\alpha $$2. Dynamics of the Entire System
Next, we find the acceleration $a$ of the system. Considering the V-groove (mass $M$), the cylinder (mass $m$), and the hanging weight (mass $m_1$) as a single system, the total mass is $M_{total} = M + m + m_1$. The net external force driving the motion is the weight of $m_1$.
Applying Newton's second law to the entire system:
$$ F_{net} = M_{total} a $$ $$ m_1 g = (M + m + m_1) a $$Solving for the acceleration $a$:
$$ a = \frac{m_1 g}{M + m + m_1} $$3. Condition on Mass $m_1$
Finally, we combine the two results by substituting the expression for $a$ into the inequality condition:
$$ \frac{m_1 g}{M + m + m_1} \le g \tan\alpha $$We cancel $g$ and solve for $m_1$:
$$ m_1 \le (M + m + m_1) \tan\alpha $$ $$ m_1 \le (M+m)\tan\alpha + m_1 \tan\alpha $$ $$ m_1 (1 - \tan\alpha) \le (M+m)\tan\alpha $$Since it is given that $\alpha < 45^\circ$, we have $\tan\alpha < 1$, which means $1 - \tan\alpha > 0$. Therefore, we can divide by $(1 - \tan\alpha)$ without changing the direction of the inequality:
$$ m_1 \le \frac{(M+m)\tan\alpha}{1 - \tan\alpha} $$This is the condition that $m_1$ must satisfy for the cylinder to not leave the V-shaped groove.