Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in the diagram, a cart with mass $M$ is on a horizontal surface. On top of the cart, there is an object with mass $m_1$. A string connects $m_1$ to another object with mass $m_2$ which hangs over a pulley attached to the cart. The known masses are $M = 51$ kg, $m_1 = 5$ kg, and $m_2 = 4$ kg. The masses of the pulley, the supporting rod, and the inextensible string are negligible. All friction at contact surfaces is also ignored. A horizontal force $F$ is applied to the cart.
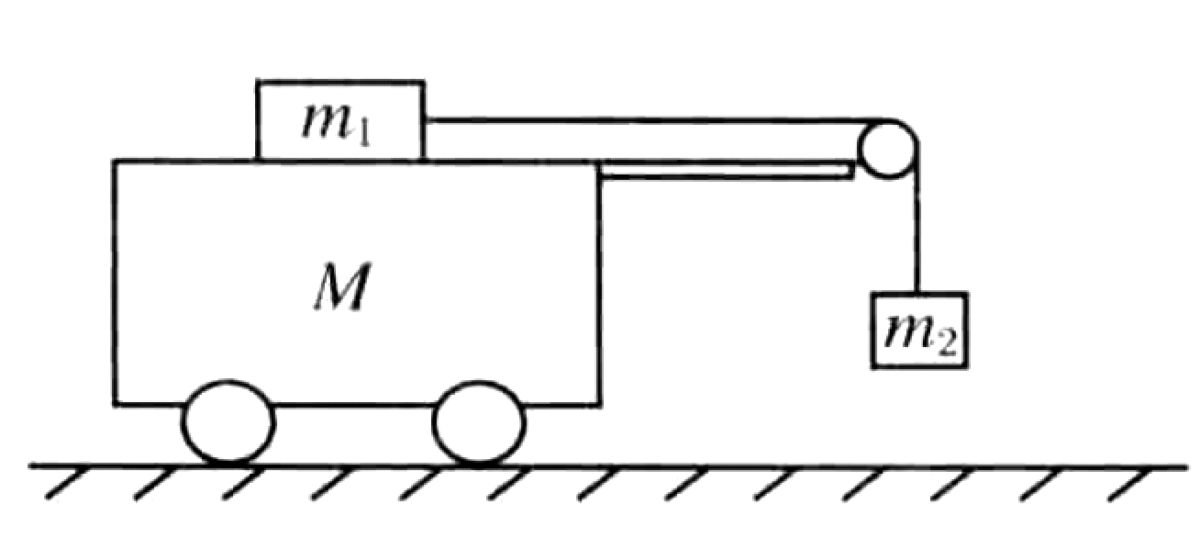
01K5Z1MF1A3MZWPT237B4HKA3Z
The magnitude of the horizontal force $F$ required is given by the expression:
$$F = (M + m_1 + m_2)\left(\frac{m_2}{m_1}g\right)$$Substituting the given values:
$$F = 470.4 \text{ N}$$The problem asks for the magnitude of the horizontal force $F$ required to ensure there is no relative motion between the objects $m_1$ and $m_2$. The condition of "no relative motion" implies that the entire system (cart $M$, mass $m_1$, and mass $m_2$) moves together with a common horizontal acceleration, $a$. Furthermore, it implies that mass $m_2$ has zero vertical acceleration.
We will apply Newton's second law to the components of the system in an inertial frame of reference (the ground).
-
Analyze mass $m_2$: The forces acting on $m_2$ are the gravitational force $m_2g$ downwards and the tension $T$ from the string upwards. Since there is no relative vertical motion, its vertical acceleration is zero. Applying Newton's second law in the vertical direction for $m_2$:
$$T - m_2g = 0$$ $$T = m_2g$$ -
Analyze mass $m_1$: The only horizontal force acting on $m_1$ is the tension $T$ from the string (friction is ignored). Since $m_1$ moves with the cart, its horizontal acceleration is $a$. Applying Newton's second law in the horizontal direction for $m_1$:
$$T = m_1 a$$ -
Determine the common acceleration $a$: By equating the two expressions for tension $T$ from steps 1 and 2, we can find the required acceleration of the system.
$$m_1 a = m_2g$$ $$a = \frac{m_2}{m_1}g$$ -
Determine the applied force $F$: Now, consider the entire system, composed of masses $M$, $m_1$, and $m_2$, as a single object of total mass $M_{total} = M + m_1 + m_2$. The only external horizontal force acting on this combined system is $F$. Applying Newton's second law to the entire system:
$$F = (M + m_1 + m_2)a$$Substituting the expression for $a$ from step 3:
$$F = (M + m_1 + m_2)\left(\frac{m_2}{m_1}g\right)$$ -
Substitute numerical values: Given $M = 51$ kg, $m_1 = 5$ kg, $m_2 = 4$ kg, and using the standard gravitational acceleration $g = 9.8 \text{ m/s}^2$:
$$F = (51 \text{ kg} + 5 \text{ kg} + 4 \text{ kg})\left(\frac{4 \text{ kg}}{5 \text{ kg}}(9.8 \text{ m/s}^2)\right)$$ $$F = (60 \text{ kg})(0.8 \times 9.8 \text{ m/s}^2)$$ $$F = (60 \text{ kg})(7.84 \text{ m/s}^2)$$ $$F = 470.4 \text{ N}$$