Source: High school physics (Chinese)
Problem Sets:
Problem
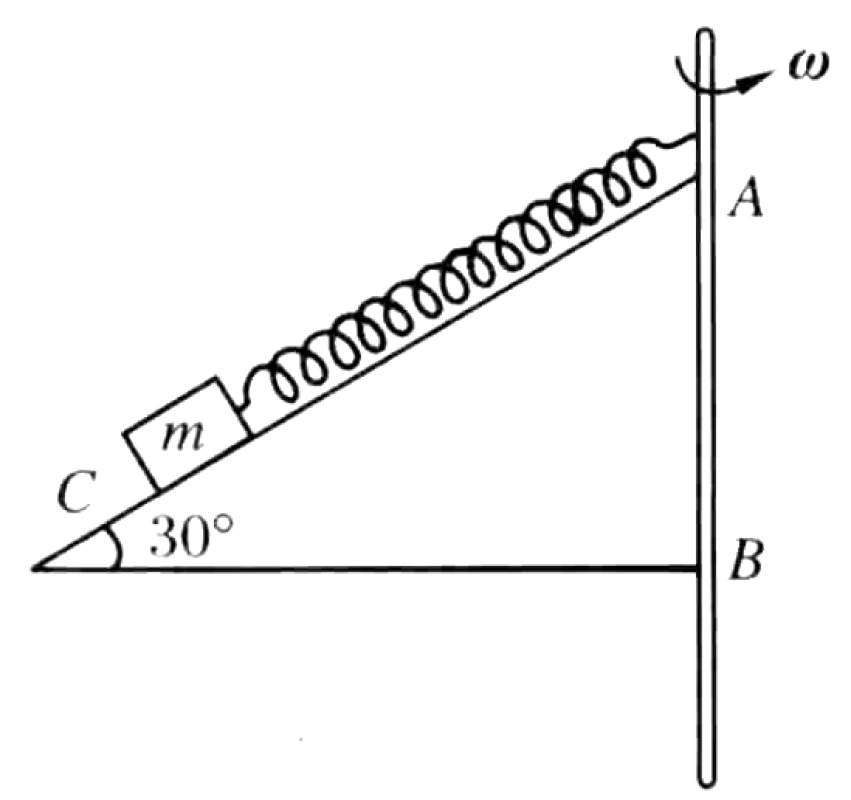
A block C of mass $m = 2$ kg is placed on a smooth inclined plane with an angle of inclination $\alpha = 30^\circ$. It is attached to a light spring with an unstretched length of $l_0 = 0.2$ m. The other end of the spring is fixed at the top of the incline. When the system is at rest, the spring stretches to a length of $l_1 = 0.25$ m. The entire system (incline and block) rotates about a vertical axis AB as shown. (Use $g = 9.8$ m/s²)
- What is the length of the spring when the rotation speed is $n = 60$ rev/min?
- At what rotation speed (in rev/min) does the block C exert no normal force on the inclined plane?
01K5Z15K2ZRZM1FNM8A2DKPKAV
[Q1] The length of the spring is $l_2 = \frac{kl_1}{k - m\omega^2\cos^2\alpha} \approx 0.358$ m. [Q2] The rotation speed at which the block exerts no normal force is $n = \frac{30}{\pi}\sqrt{\frac{g}{l_0\sin\alpha + mg/k}} \approx 66.85$ rev/min.
Based on the problem description and diagram, the inclined plane slopes downwards and away from the vertical axis of rotation AB. The block C moves along the hypotenuse AC.
1. Spring Constant, $k$ In the static case (no rotation), the block is in equilibrium. The forces along the incline are the spring force $F_{s1}$ and the component of gravity $mg\sin\alpha$.
$$F_{s1} - mg\sin\alpha = 0$$Using Hooke's law, $F_{s1} = k(l_1 - l_0)$:
$$k(l_1 - l_0) = mg\sin\alpha$$Solving for the spring constant $k$:
$$k = \frac{mg\sin\alpha}{l_1 - l_0}$$Substituting the given values:
$m = 2$ kg, $g = 9.8$ m/s², $\alpha = 30^\circ$, $l_1 = 0.25$ m, $l_0 = 0.2$ m. $$k = \frac{(2 \text{ kg})(9.8 \text{ m/s}^2)\sin(30^\circ)}{0.25 \text{ m} - 0.2 \text{ m}} = \frac{9.8 \text{ N}}{0.05 \text{ m}} = 196 \text{ N/m}$$[Q1] Spring Length at $n = 60$ rev/min When the system rotates, we analyze the forces in a non-inertial frame rotating with the block. The block is in equilibrium under gravity, normal force, spring force, and the fictitious centrifugal force $F_{cf}$. Let's balance forces along the incline (positive down the incline). The component of gravity is $mg\sin\alpha$. The spring force is $F_s = k(l_2-l_0)$ (up the incline). The centrifugal force is $F_{cf} = m\omega^2 r$ (horizontally outwards), where $r = l_2\cos\alpha$. Its component along the incline is $F_{cf}\cos\alpha$. The equilibrium equation along the incline is:
$$mg\sin\alpha + F_{cf}\cos\alpha - F_s = 0$$ $$mg\sin\alpha + (m\omega^2 l_2\cos\alpha)\cos\alpha - k(l_2 - l_0) = 0$$Rearranging to solve for the new length $l_2$:
$$mg\sin\alpha + kl_0 = l_2(k - m\omega^2\cos^2\alpha)$$ $$l_2 = \frac{mg\sin\alpha + kl_0}{k - m\omega^2\cos^2\alpha}$$From the static case, we know $mg\sin\alpha = k(l_1 - l_0)$, so $kl_0 + mg\sin\alpha = kl_0 + k(l_1-l_0) = kl_1$.
$$l_2 = \frac{kl_1}{k - m\omega^2\cos^2\alpha}$$The rotation speed is $n = 60$ rev/min. The angular velocity $\omega$ is:
$$\omega = 60 \frac{\text{rev}}{\text{min}} \times \frac{2\pi \text{ rad}}{1 \text{ rev}} \times \frac{1 \text{ min}}{60 \text{ s}} = 2\pi \text{ rad/s}$$Substituting the values:
$$l_2 = \frac{(196 \text{ N/m})(0.25 \text{ m})}{196 \text{ N/m} - (2 \text{ kg})(2\pi \text{ rad/s})^2 \cos^2(30^\circ)} = \frac{49}{196 - 8\pi^2(3/4)} = \frac{49}{196 - 6\pi^2}$$ $$l_2 = \frac{49}{196 - 6(9.8696)} = \frac{49}{136.7824} \approx 0.3582 \text{ m}$$[Q2] Speed for Zero Normal Force The block exerts no normal force on the plane when $N=0$. We balance the forces perpendicular to the incline. The component of gravity is $mg\cos\alpha$ (into the incline). The centrifugal force component is $F_{cf}\sin\alpha$ (out of the incline). The equilibrium equation perpendicular to the incline is:
$$N - mg\cos\alpha + F_{cf}\sin\alpha = 0$$ $$N = mg\cos\alpha - m\omega^2 r \sin\alpha$$Setting $N=0$ gives the condition for the block to lift off:
$$mg\cos\alpha = m\omega^2 r \sin\alpha = m\omega^2 (l\cos\alpha) \sin\alpha$$ $$g = \omega^2 l \sin\alpha \implies \omega^2 = \frac{g}{l\sin\alpha}$$At this point, the spring length $l$ is determined by the force balance along the incline. From Q1, we have $F_s = mg\sin\alpha + m\omega^2 r \cos\alpha$. Substituting $\omega^2 r = g/\tan\alpha$:
$$F_s = mg\sin\alpha + m(g/\tan\alpha)\cos\alpha = mg\sin\alpha + mg\frac{\cos^2\alpha}{\sin\alpha} = \frac{mg}{\sin\alpha}$$Using Hooke's Law, $F_s = k(l-l_0)$:
$$k(l-l_0) = \frac{mg}{\sin\alpha} \implies l = l_0 + \frac{mg}{k\sin\alpha}$$Now substitute this $l$ into the expression for $\omega^2$:
$$\omega^2 = \frac{g}{\left(l_0 + \frac{mg}{k\sin\alpha}\right)\sin\alpha} = \frac{g}{l_0\sin\alpha + \frac{mg}{k}}$$Substituting values:
$$\omega^2 = \frac{9.8}{0.2\sin(30^\circ) + \frac{2 \times 9.8}{196}} = \frac{9.8}{0.2(0.5) + 0.1} = \frac{9.8}{0.2} = 49 \text{ (rad/s)}^2$$ $$\omega = 7 \text{ rad/s}$$Converting to rev/min:
$$n = \omega \times \frac{60}{2\pi} = 7 \times \frac{30}{\pi} = \frac{210}{\pi} \approx 66.85 \text{ rev/min}$$