Source: High school physics (Chinese)
Problem Sets:
Problem
An object of mass $m$ is placed on the conical surface of an umbrella. The cone surface makes an angle $\theta$ with the horizontal. The umbrella rotates about its vertical axis with a constant angular velocity $\omega$. The object is at a horizontal distance $r$ from the axis of rotation.
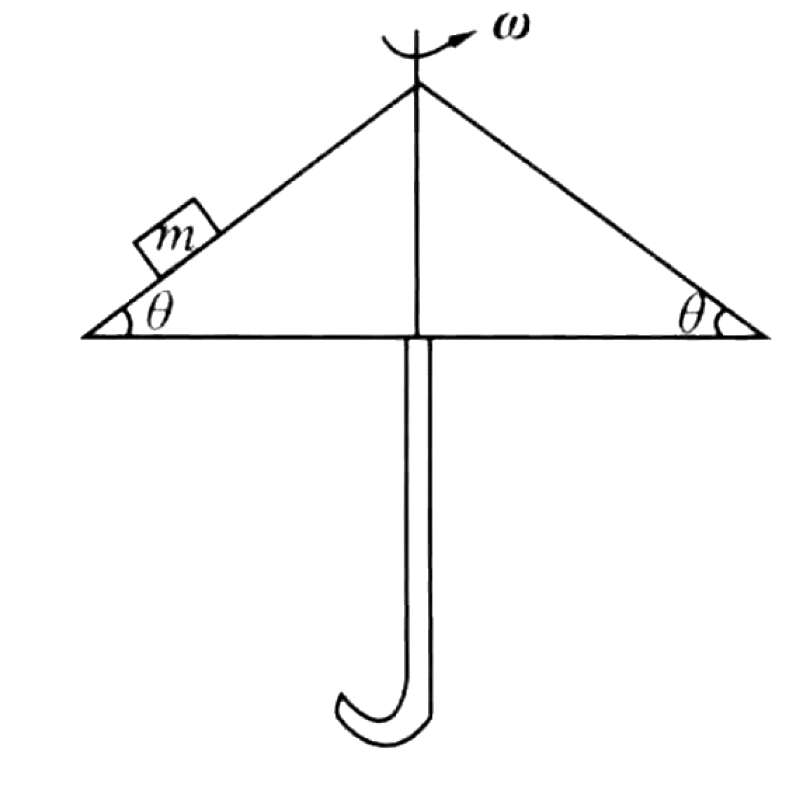
01K5Z12Z37DT5670CMR7EGPD6Q
The minimum coefficient of static friction $\mu$ required is:
$$ \mu = \frac{g\sin\theta - \omega^2 r \cos\theta}{g\cos\theta + \omega^2 r \sin\theta} $$To find the minimum coefficient of static friction $\mu$ to prevent the object from sliding down, we analyze the forces acting on the object in a stationary reference frame. The object is in uniform circular motion, so the net force must provide the required centripetal acceleration, $a_c = \omega^2 r$, directed horizontally towards the axis of rotation.
The forces acting on the object are:
- Gravitational force, $F_g = mg$, acting vertically downward.
- Normal force, $N$, perpendicular to the conical surface.
- Static friction force, $f_s$, parallel to the surface. To prevent the object from sliding down, this force must be directed up the incline. For the minimum coefficient, the friction is at its maximum value, $f_s = \mu N$.
We apply Newton's second law by resolving forces into horizontal and vertical components.
Vertical forces (no acceleration): The sum of vertical forces is zero. The upward components of the normal force and friction balance the downward gravitational force.
$$ \sum F_y = N \cos\theta + f_s \sin\theta - mg = 0 $$Substituting $f_s = \mu N$:
$$ N(\cos\theta + \mu \sin\theta) = mg \quad (1) $$Horizontal forces (centripetal acceleration): The net horizontal force provides the centripetal acceleration, $a_c = \omega^2 r$. The horizontal component of the normal force points towards the center, while the horizontal component of friction points away.
$$ \sum F_x = N \sin\theta - f_s \cos\theta = m a_c = m \omega^2 r $$Substituting $f_s = \mu N$:
$$ N(\sin\theta - \mu \cos\theta) = m \omega^2 r \quad (2) $$Now, we solve for $\mu$ by dividing equation (2) by equation (1) to eliminate $N$:
$$ \frac{N(\sin\theta - \mu \cos\theta)}{N(\cos\theta + \mu \sin\theta)} = \frac{m \omega^2 r}{mg} $$ $$ \frac{\sin\theta - \mu \cos\theta}{\cos\theta + \mu \sin\theta} = \frac{\omega^2 r}{g} $$To isolate $\mu$, we cross-multiply:
$$ g(\sin\theta - \mu \cos\theta) = \omega^2 r (\cos\theta + \mu \sin\theta) $$ $$ g\sin\theta - g\mu\cos\theta = \omega^2 r \cos\theta + \omega^2 r \mu\sin\theta $$Group the terms containing $\mu$:
$$ g\sin\theta - \omega^2 r \cos\theta = \mu (g\cos\theta + \omega^2 r \sin\theta) $$Solving for $\mu$:
$$ \mu = \frac{g\sin\theta - \omega^2 r \cos\theta}{g\cos\theta + \omega^2 r \sin\theta} $$This expression is valid provided that the numerator is non-negative, i.e., $g\sin\theta \ge \omega^2 r \cos\theta$. If the numerator is negative, the object has a tendency to slide up, and no friction is needed to prevent it from sliding down ($\mu=0$).