Source: High school physics (Chinese)
Problem
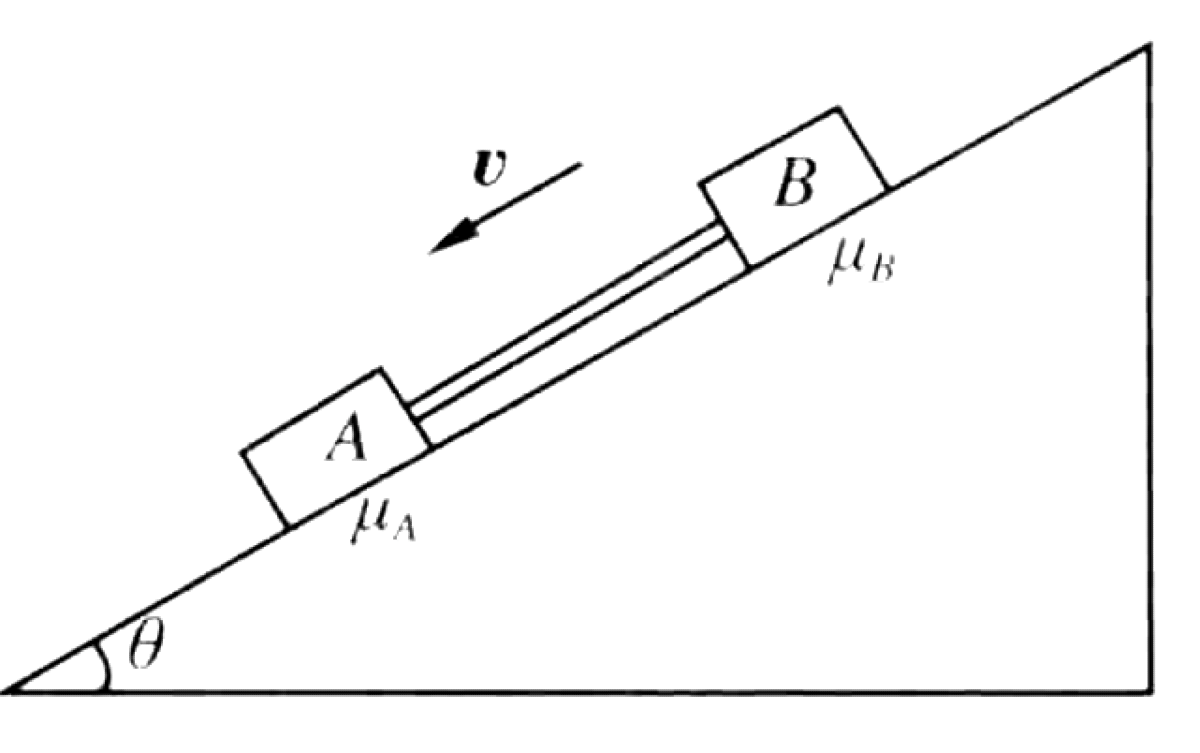
Two blocks, A and B, with masses $m_A$ and $m_B$ and coefficients of kinetic friction $\mu_A$ and $\mu_B$ respectively, are connected by a light rod. They slide down an inclined plane with an angle of inclination $\theta$ together, as shown in the figure. It is assumed that the condition for sliding down is met, i.e., $\tan\theta > \mu_A$ and $\tan\theta > \mu_B$.
- In the case where $\mu_A > \mu_B$, determine if there is a force in the rod. If so, find its magnitude and direction.
- In the case where $\mu_A = \mu_B$, determine if there is a force in the rod. If so, find its magnitude and direction.
- In the case where $\mu_A < \mu_B$, determine if there is a force in the rod. If so, find its magnitude and direction.
01K5Z101CV91G3C1RY4XQN7R9R
[Q1] For $\mu_A > \mu_B$: Yes, there is a force in the rod. The rod is in compression. Its magnitude is:
$$F_C = \frac{m_A m_B g\cos\theta}{m_A+m_B}(\mu_A - \mu_B)$$[Q2] For $\mu_A = \mu_B$: No, there is no force in the rod.
$$F = 0$$[Q3] For $\mu_A < \mu_B$: Yes, there is a force in the rod. The rod is in tension. Its magnitude is:
$$F_T = \frac{m_A m_B g\cos\theta}{m_A+m_B}(\mu_B - \mu_A)$$Let the positive x-axis be directed down the inclined plane. Since the blocks slide together, they share a common acceleration, $a$. Let $F_{rod}$ be the force exerted by the rod on block A. A positive $F_{rod}$ indicates a force down the incline (compression), and a negative $F_{rod}$ indicates a force up the incline (tension).
First, we find the common acceleration by considering both blocks as a single system with mass $M = m_A + m_B$. The net force along the incline is the sum of the gravitational components minus the total friction force. The gravitational force component is $(m_A+m_B)g\sin\theta$. The total friction force is $f_k = f_{kA} + f_{kB} = \mu_A N_A + \mu_B N_B = (\mu_A m_A + \mu_B m_B)g\cos\theta$.
Applying Newton's second law to the system:
$$ (m_A+m_B)g\sin\theta - (\mu_A m_A + \mu_B m_B)g\cos\theta = (m_A+m_B)a $$Solving for the acceleration $a$:
$$ a = g\sin\theta - \frac{\mu_A m_A + \mu_B m_B}{m_A+m_B}g\cos\theta $$Next, we analyze the forces on block A to find $F_{rod}$. The forces on block A along the incline are its component of gravity ($m_A g\sin\theta$), its friction force ($f_{kA} = \mu_A m_A g\cos\theta$), and the force from the rod ($F_{rod}$). Applying Newton's second law to block A:
$$ m_A g\sin\theta - \mu_A m_A g\cos\theta + F_{rod} = m_A a $$Solving for $F_{rod}$:
$$ F_{rod} = m_A a - (m_A g\sin\theta - \mu_A m_A g\cos\theta) $$Substitute the expression for $a$:
$$ F_{rod} = m_A \left( g\sin\theta - \frac{\mu_A m_A + \mu_B m_B}{m_A+m_B}g\cos\theta \right) - m_A(g\sin\theta - \mu_A g\cos\theta) $$ $$ F_{rod} = m_A g\cos\theta \left( -\frac{\mu_A m_A + \mu_B m_B}{m_A+m_B} + \mu_A \right) $$ $$ F_{rod} = \frac{m_A g\cos\theta}{m_A+m_B} [-\mu_A m_A - \mu_B m_B + \mu_A(m_A+m_B)] $$ $$ F_{rod} = \frac{m_A g\cos\theta}{m_A+m_B} [-\mu_A m_A - \mu_B m_B + \mu_A m_A + \mu_A m_B] $$This simplifies to the general expression for the force in the rod:
$$ F_{rod} = \frac{m_A m_B g\cos\theta}{m_A+m_B}(\mu_A - \mu_B) $$We now analyze this result for the three given cases.
[Q1] In the case where $\mu_A > \mu_B$: The term $(\mu_A - \mu_B)$ is positive. Since all other quantities in the expression are positive, $F_{rod} > 0$. A positive $F_{rod}$ represents a force on block A directed down the incline, meaning the rod is pushing on block A. Therefore, the rod is in compression. The magnitude of the compressive force is:
$$ F_C = \frac{m_A m_B g\cos\theta}{m_A+m_B}(\mu_A - \mu_B) $$[Q2] In the case where $\mu_A = \mu_B$: The term $(\mu_A - \mu_B)$ is zero. Therefore, $F_{rod} = 0$. There is no force in the rod.
[Q3] In the case where $\mu_A < \mu_B$: The term $(\mu_A - \mu_B)$ is negative. Therefore, $F_{rod} < 0$. A negative $F_{rod}$ represents a force on block A directed up the incline, meaning the rod is pulling on block A. Therefore, the rod is in tension. The magnitude of the tensile force is:
$$ F_T = |F_{rod}| = \frac{m_A m_B g\cos\theta}{m_A+m_B}(\mu_B - \mu_A) $$