Source: High school physics (Chinese)
Problem
A triangular wooden block ABC rests on a rough horizontal surface. On its two rough inclined surfaces, two blocks with masses $m_1$ and $m_2$ ($m_1 > m_2$) are placed, as shown in Figure. The angles of inclination are $\theta_1$ and $\theta_2$. The entire system, consisting of the triangular block and the two smaller blocks, is at rest.
- Is there a friction force exerted by the horizontal surface on the triangular block?
- If there is a friction force, what is its direction?
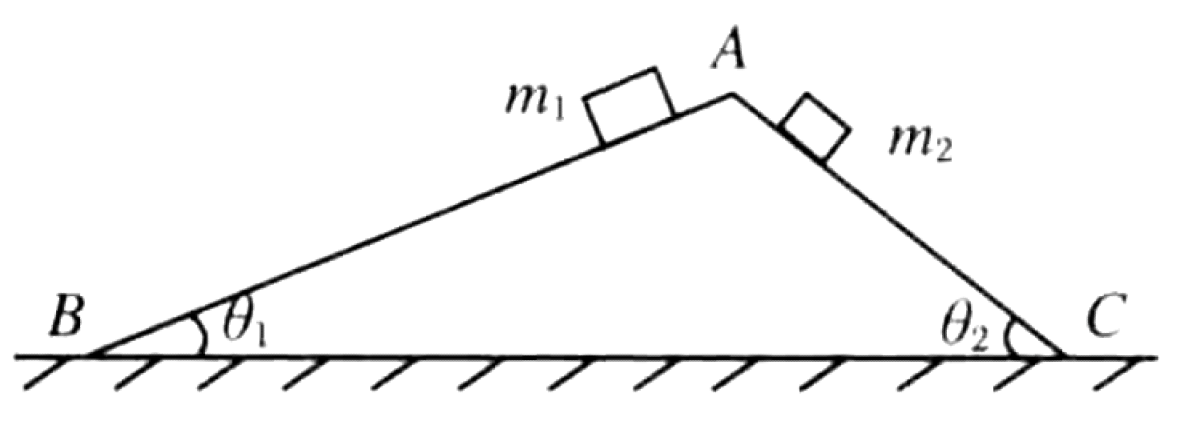
01K5Z0VJVKNRWNQ67BRYM8WHEH
[Q1] No, there is no friction force exerted by the horizontal surface on the triangular block. The net horizontal force exerted by the two small blocks on the wedge is zero. [Q2] Since the friction force is zero, it has no direction.
Analysis of Forces
The core of this problem lies in analyzing the forces exchanged between the small blocks and the wedge. Since the entire system is at rest, each component is in static equilibrium.
-
Force Exerted by a Block on the Wedge: Let's consider block $m_1$. It is in equilibrium under the influence of two forces: its weight $\vec{W}_1 = m_1\vec{g}$ (acting vertically downwards) and the total force exerted by the wedge on it, $\vec{F}_{\text{wedge on 1}}$. For equilibrium, the net force on $m_1$ must be zero:
$$ \vec{W}_1 + \vec{F}_{\text{wedge on 1}} = 0 $$This implies that the force from the wedge on the block is equal and opposite to the block's weight:
$$ \vec{F}_{\text{wedge on 1}} = -\vec{W}_1 $$By Newton's third law, the force exerted by block $m_1$ on the wedge, $\vec{F}_{\text{1 on wedge}}$, is equal and opposite to the force the wedge exerts on the block:
$$ \vec{F}_{\text{1 on wedge}} = - \vec{F}_{\text{wedge on 1}} = -(-\vec{W}_1) = \vec{W}_1 $$This shows that the total force exerted by block $m_1$ on the wedge is simply equal to its own weight, $m_1\vec{g}$, a purely vertical force acting downwards. This total force is the vector sum of the normal force and the static friction force between the block and the wedge.
-
Horizontal Equilibrium of the Wedge: The same logic applies to block $m_2$. The total force it exerts on the wedge is equal to its weight, $\vec{W}_2 = m_2\vec{g}$, which is also a purely vertical force. Therefore, the two blocks $m_1$ and $m_2$ only exert vertical forces on the wedge. They exert no net horizontal force.
Now, consider the wedge in equilibrium. The external horizontal forces acting on the wedge are the horizontal forces from the blocks and the static friction force from the ground, $f_g$.
$$ \sum F_{\text{horizontal}} = (F_{\text{1 on wedge}})_x + (F_{\text{2 on wedge}})_x + f_g = 0 $$As we have shown, the horizontal components of the forces from the blocks are zero:
$$ 0 + 0 + f_g = 0 \implies f_g = 0 $$
Conclusion: The static friction forces on the inclined planes adjust themselves perfectly to ensure that the total force from each block on the wedge is directed vertically. Consequently, there is no net horizontal push on the wedge, and no static friction is required from the horizontal surface to maintain equilibrium.
Verification via Components: For block $m_1$ to be at rest, the forces along the incline must balance, and forces perpendicular to the incline must balance.
- Force perpendicular to incline: The normal force from the wedge on the block is $N'_1 = m_1g\cos\theta_1$.
- Force parallel to incline: The static friction from the wedge on the block is $f'_1 = m_1g\sin\theta_1$ (up the incline).
By Newton's third law, the block exerts forces of the same magnitude on the wedge: a normal force $N_1 = m_1g\cos\theta_1$ (into the wedge) and a friction force $f_1 = m_1g\sin\theta_1$ (down the incline).
The net horizontal force on the wedge from block $m_1$ is the sum of the horizontal components of $N_1$ and $f_1$.
- Horizontal component of $N_1$: $N_1\sin\theta_1$ (to the right, based on the diagram).
- Horizontal component of $f_1$: $-f_1\cos\theta_1$ (to the left, based on the diagram). Total horizontal force from $m_1$:
A similar calculation for block $m_2$ also yields a zero net horizontal force. This confirms the conceptual result.