Source: High school physics (Chinese)
Problem
As shown in Figure, two objects, A and B, have masses $m_A$ and $m_B$. They are in contact along a smooth surface that makes an angle $\alpha$ with the horizontal. Both blocks are on a horizontal surface, and the coefficient of kinetic friction between each block and the ground is $\mu$. A horizontal force $F$ pushes block A, causing A and B to accelerate together.
- Find the interaction force between A and B.
- To maintain A and B moving together without relative motion, what is the allowed range for the value of F?
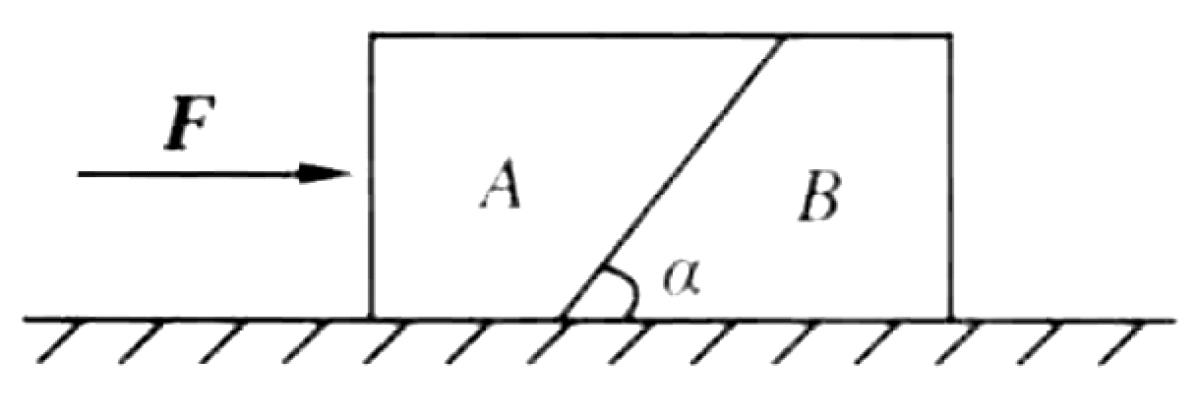
01K5Z0T5YVVF3K4CXG7XARR1TY
[Q1] The interaction force between A and B is:
$$N_{AB} = \frac{m_B F}{(m_A+m_B)(\sin\alpha - \mu\cos\alpha)}$$[Q2] For the blocks to move together, it is required that $\tan\alpha > \mu$. If this condition is met, the allowed range for the force $F$ is:
$$\mu(m_A+m_B)g < F \le \frac{m_A(m_A+m_B)g}{m_B}(\tan\alpha - \mu)$$System Analysis First, we analyze the two blocks A and B as a single system of total mass $M = m_A + m_B$. The system moves horizontally with a common acceleration $a$. Applying Newton's second law in the horizontal direction:
$$F - f_k = (m_A + m_B)a$$The total kinetic friction force is $f_k = \mu N_{total} = \mu(m_A+m_B)g$.
$$F - \mu(m_A+m_B)g = (m_A+m_B)a$$This gives the acceleration of the system:
$$a = \frac{F}{m_A+m_B} - \mu g$$[Q1] Interaction Force between A and B Let $N_{AB}$ be the magnitude of the normal force exerted by A on B. This force is perpendicular to the contact surface. We analyze the forces on block B. The forces acting on block B are:
- Weight $m_B g$ (downward).
- Normal force from the ground $N_B$ (upward).
- Kinetic friction from the ground $f_B = \mu N_B$ (leftward).
- Interaction force from A, $N_{AB}$. This force has a horizontal component $N_{AB}\sin\alpha$ (rightward) and a vertical component $N_{AB}\cos\alpha$ (downward).
Applying Newton's second law to block B:
- Vertical equilibrium ($\sum F_y = 0$):
- Horizontal motion ($\sum F_x = m_B a$):
Substitute the expression for $N_B$ into the horizontal equation:
$$N_{AB}\sin\alpha - \mu(m_B g + N_{AB}\cos\alpha) = m_B a$$Rearranging to solve for $N_{AB}$:
$$N_{AB}(\sin\alpha - \mu\cos\alpha) = m_B(a + \mu g)$$From the system analysis, we have $a + \mu g = \frac{F}{m_A+m_B}$. Substituting this in:
$$N_{AB}(\sin\alpha - \mu\cos\alpha) = m_B \left(\frac{F}{m_A+m_B}\right)$$The interaction force is:
$$N_{AB} = \frac{m_B F}{(m_A+m_B)(\sin\alpha - \mu\cos\alpha)}$$[Q2] Allowed Range for F For the blocks to move together as described, three conditions must be met:
-
The blocks must accelerate: $a > 0$.
$$ \frac{F}{m_A+m_B} - \mu g > 0 \implies F > \mu(m_A+m_B)g $$This sets the minimum force required.
-
The blocks must remain in contact: $N_{AB} > 0$. Since $F$, $m_A$, and $m_B$ are positive, this requires the denominator of the $N_{AB}$ expression to be positive:
$$ \sin\alpha - \mu\cos\alpha > 0 \implies \tan\alpha > \mu $$This is a necessary condition on the system parameters for this type of motion to be possible.
-
Block A must not lift off the ground: The normal force on A from the ground, $N_A$, must be non-negative ($N_A \ge 0$). We analyze the vertical forces on block A. The interaction force from B on A, $N_{BA}$, is equal in magnitude to $N_{AB}$ and acts with an upward vertical component $N_{BA}\cos\alpha$. Vertical equilibrium for block A:
$$N_A - m_A g + N_{BA}\cos\alpha = 0 \implies N_A = m_A g - N_{AB}\cos\alpha$$The condition $N_A \ge 0$ implies:
$$m_A g \ge N_{AB}\cos\alpha$$Substitute the expression for $N_{AB}$:
$$m_A g \ge \frac{m_B F \cos\alpha}{(m_A+m_B)(\sin\alpha - \mu\cos\alpha)}$$Solving for $F$ gives the maximum allowed force:
$$F \le \frac{m_A g (m_A+m_B)(\sin\alpha - \mu\cos\alpha)}{m_B \cos\alpha}$$ $$F \le \frac{m_A(m_A+m_B)g}{m_B}(\tan\alpha - \mu)$$(Note: The normal force on B, $N_B = m_B g + N_{AB}\cos\alpha$, is always positive, so B never lifts off.)
Combining the conditions on $F$, the allowed range is:
$$\mu(m_A+m_B)g < F \le \frac{m_A(m_A+m_B)g}{m_B}(\tan\alpha - \mu)$$