Source: High school physics (Chinese)
Problem
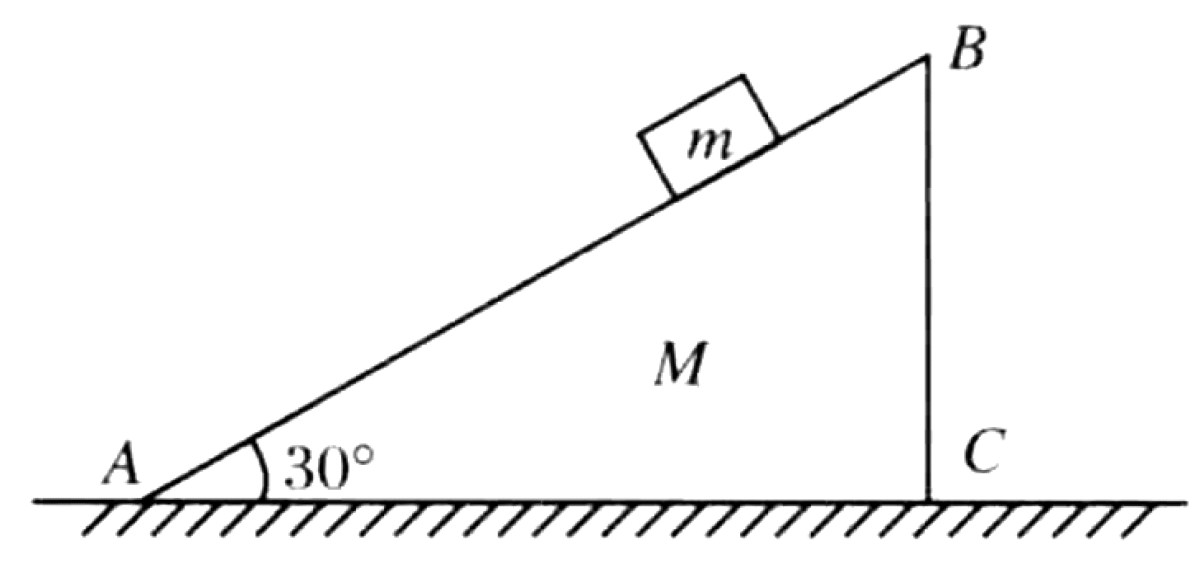
As shown in Figure, a wooden wedge ABC with mass $M=10$ kg is stationary on a rough horizontal ground. A block with mass $m=1.0$ kg starts to slide down from rest on the inclined surface of the wedge, which has an angle $\theta = 30^\circ$. When the block has slid a distance $s=1.4$ m, its velocity is $v=1.4$ m/s. Throughout this process, the wedge does not move. The gravitational acceleration is $g=10$ m/s². The coefficient of kinetic friction between the wedge and the ground is given as $\mu=0.02$, though this information might not be necessary for the primary calculation.
- Find the magnitude of the friction force exerted by the ground on the wedge.
- Find the direction of the friction force exerted by the ground on the wedge.
01K5Z0CG2VRSRXB6HAQZ8AMSN7
[Q1] The magnitude of the friction force exerted by the ground on the wedge is given by the formula $f_s = ma \cos\theta$. Numerically, this is:
$$f_s = 0.35\sqrt{3} \text{ N} \approx 0.61 \text{ N}$$[Q2] The direction of the friction force exerted by the ground on the wedge is to the left, opposing the tendency of motion of the wedge.
To solve this problem, we analyze the forces acting on the system composed of the block and the wedge.
1. Acceleration of the Block
First, we determine the acceleration a of the block m as it slides down the wedge. The block starts from rest ($v_0=0$) and reaches a velocity v after traveling a distance s. We can use the kinematic equation:
Solving for the acceleration a:
Substituting the given values:
$s = 1.4$ m, $v = 1.4$ m/s. $$a = \frac{(1.4 \text{ m/s})^2}{2(1.4 \text{ m})} = \frac{1.4}{2} \text{ m/s}^2 = 0.7 \text{ m/s}^2$$2. System Dynamics and Friction Force
[Q1] To find the friction force exerted by the ground on the wedge, we consider the block and the wedge as a single system. The wedge is stationary, so its acceleration is zero. The block has an acceleration a directed down the inclined plane.
Let's apply Newton's second law for a system of particles in the horizontal direction:
$$\sum F_{\text{ext}, x} = m a_{m,x} + M a_{M,x}$$where:
- $\sum F_{\text{ext}, x}$ is the sum of external horizontal forces on the system. The only external horizontal force is the static friction from the ground on the wedge, $f_s$.
- $a_{m,x}$ is the horizontal component of the block's acceleration.
- $a_{M,x}$ is the horizontal component of the wedge's acceleration, which is zero since the wedge is stationary.
From the figure, the block slides down and to the left. Let's define the positive x-axis to the right. The block's acceleration vector a points down the incline at an angle \theta to the horizontal. Its horizontal component is:
The negative sign indicates the acceleration is to the left.
Substituting into Newton's second law:
$$f_{s,x} = m(-a \cos\theta) + M(0)$$ $$f_{s,x} = -ma \cos\theta$$The magnitude of the friction force is therefore:
$$f_s = |f_{s,x}| = ma \cos\theta$$Now, we substitute the numerical values:
$m = 1.0$ kg, $a = 0.7$ m/s², $\theta = 30^\circ$. $$f_s = (1.0 \text{ kg})(0.7 \text{ m/s}^2) \cos(30^\circ) = 0.7 \times \frac{\sqrt{3}}{2} \text{ N}$$ $$f_s = 0.35\sqrt{3} \text{ N} \approx 0.61 \text{ N}$$[Q2] The direction of the friction force is given by the sign of $f_{s,x}$. Since $m, a, \cos\theta$ are all positive, $f_{s,x}$ is negative. This means the friction force exerted by the ground on the wedge points in the negative x-direction, which is to the left.
This result is counter-intuitive. One might expect the block sliding left to push the wedge left, requiring a friction force to the right. However, a detailed analysis shows the block's acceleration causes the wedge to be pushed to the right, necessitating a friction force to the left. The force the block exerts on the wedge has a horizontal component ma cos(theta) to the right. The static friction must balance this, so it acts to the left with the same magnitude.