Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in Figure, a small block is placed on a fixed inclined plane with an inclination angle of $\theta$. The coefficient of friction between the block and the plane is given as $\mu = \tan\varphi$, where $\varphi$ is a fixed angle. A force $F$ is applied to the block at an angle $\beta$ with respect to the inclined plane, pulling it upwards along the plane.
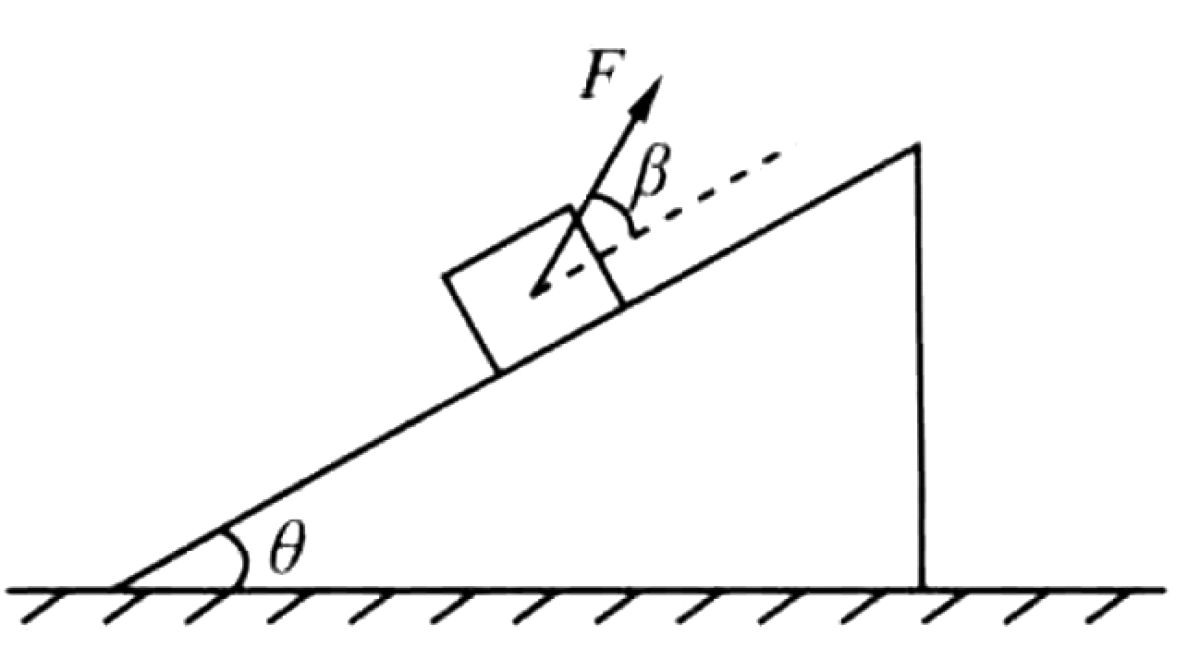
01K5Z09MQ3CTWNT39AYW3TKAHH
To minimize the force $F$ required to start moving the block, the angle $\beta$ should be equal to the angle of friction $\varphi$.
$$ \beta = \varphi $$To solve this problem, we analyze the forces acting on the block at the moment it is about to move up the incline. We use a coordinate system with the x-axis parallel to the incline (upwards) and the y-axis perpendicular to it.
Let the mass of the block be $m$ and the acceleration due to gravity be $g$. The forces acting on the block are:
- Gravitational force, $mg$, acting vertically downwards.
- Applied force, $F$, at an angle $\beta$ to the incline.
- Normal force, $N$, perpendicular to the incline.
- Maximum static friction force, $f_s$, acting down the incline.
We apply Newton's first law (condition for equilibrium) along the x and y axes.
-
Force Balance Equations Sum of forces perpendicular to the incline (y-direction):
$$ \Sigma F_y = N + F\sin\beta - mg\cos\theta = 0 $$ $$ N = mg\cos\theta - F\sin\beta $$The friction force is at its maximum value, $f_s = \mu N$.
$$ f_s = \mu (mg\cos\theta - F\sin\beta) $$Sum of forces parallel to the incline (x-direction):
$$ \Sigma F_x = F\cos\beta - mg\sin\theta - f_s = 0 $$ $$ F\cos\beta - mg\sin\theta - \mu (mg\cos\theta - F\sin\beta) = 0 $$ -
Derive the Expression for F We rearrange the equation to solve for $F$:
$$ F\cos\beta + \mu F\sin\beta = mg\sin\theta + \mu mg\cos\theta $$ $$ F(\cos\beta + \mu\sin\beta) = mg(\sin\theta + \mu\cos\theta) $$ $$ F = mg \frac{\sin\theta + \mu\cos\theta}{\cos\beta + \mu\sin\beta} $$ -
Minimize the Force F The problem states that the coefficient of friction is $\mu = \tan\varphi$. Substituting this into the expression for $F$:
$$ F = mg \frac{\sin\theta + (\tan\varphi)\cos\theta}{\cos\beta + (\tan\varphi)\sin\beta} $$By writing $\tan\varphi = \frac{\sin\varphi}{\cos\varphi}$ and multiplying the numerator and denominator by $\cos\varphi$, we get:
$$ F = mg \frac{\sin\theta\cos\varphi + \sin\varphi\cos\theta}{\cos\beta\cos\varphi + \sin\beta\sin\varphi} $$Using the trigonometric angle sum and difference identities:
$\sin(A+B) = \sin A \cos B + \cos A \sin B$ $\cos(A-B) = \cos A \cos B + \sin A \sin B$The expression for $F$ simplifies to:
$$ F = mg \frac{\sin(\theta+\varphi)}{\cos(\beta-\varphi)} $$To minimize the force $F$, the denominator $\cos(\beta-\varphi)$ must be maximized. The maximum value of the cosine function is 1. This occurs when its argument is zero.
$$ \cos(\beta-\varphi) = 1 \implies \beta - \varphi = 0 $$Therefore, the angle $\beta$ that minimizes the force $F$ is:
$$ \beta = \varphi $$
(Alternative Calculus Method) To minimize $F$, we can maximize the denominator $D(\beta) = \cos\beta + \mu\sin\beta$. Taking the derivative with respect to $\beta$ and setting it to zero:
$$ \frac{dD}{d\beta} = -\sin\beta + \mu\cos\beta = 0 $$ $$ \tan\beta = \mu $$Since $\mu = \tan\varphi$, we find that $\tan\beta = \tan\varphi$, which gives $\beta = \varphi$.