Source: High school physics (Chinese)
Problem Sets:
Problem
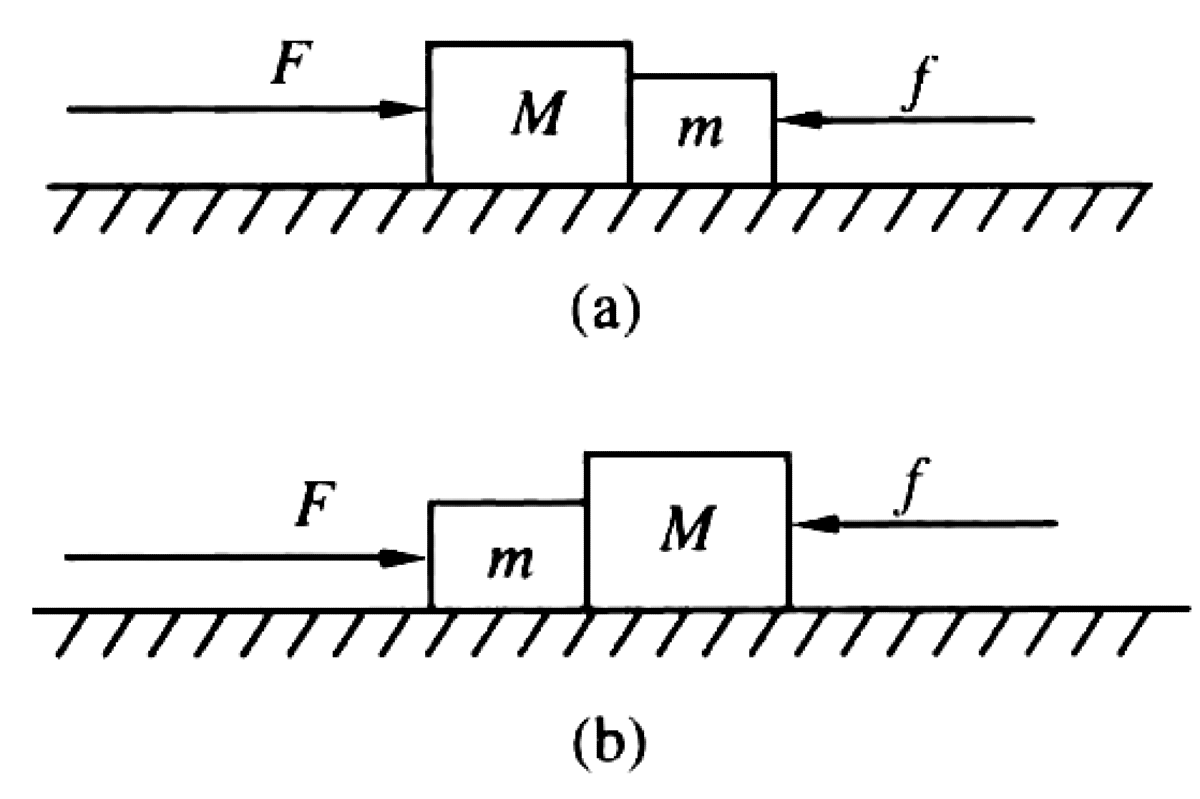
Two iron blocks are placed in contact on a smooth horizontal table. Their masses are $M = 3$ kg and $m = 2$ kg. Two horizontal forces are applied to the blocks. Force $F = 15$ N is directed to the right, and force $f = 10$ N is directed to the left.
- For the configuration shown in Figure (a), where $F$ acts on $M$ and $f$ acts on $m$, what is the contact force between the blocks?
- If the positions of $M$ and $m$ are swapped as shown in Figure (b), so that $F$ acts on $m$ and $f$ acts on $M$, what is the new contact force between the blocks?
01K5YZQ9893JGJQX9BFVYN065M
[Q1] The contact force for configuration (a) is:
$$F_{c1} = \frac{Fm + Mf}{M+m} = 12 \text{ N}$$[Q2] The contact force for configuration (b) is:
$$F_{c2} = \frac{FM + mf}{M+m} = 13 \text{ N}$$Since the blocks are in contact on a smooth surface, they move together with a common acceleration, $a$. We define the direction to the right as positive.
First, we determine the acceleration of the system by considering both blocks as a single object with total mass $(M+m)$. Applying Newton's second law to the system:
$$F - f = (M+m)a$$The acceleration of the system is:
$$a = \frac{F-f}{M+m}$$[Q1] Configuration (a)
To find the contact force $F_{c1}$, we analyze the forces on one of the blocks. Let's consider the free-body diagram for block $M$. The forces acting on it are the applied force $F$ to the right and the contact force from block $m$, $F_{c1}$, to the left. Applying Newton's second law to block $M$:
$$F - F_{c1} = Ma$$Solving for the contact force $F_{c1}$:
$$F_{c1} = F - Ma$$Substituting the expression for acceleration $a$:
$$F_{c1} = F - M\left(\frac{F-f}{M+m}\right) = \frac{F(M+m) - M(F-f)}{M+m}$$ $$F_{c1} = \frac{FM + Fm - MF + Mf}{M+m} = \frac{Fm + Mf}{M+m}$$Now, we substitute the given values: $M = 3$ kg, $m = 2$ kg, $F = 15$ N, and $f = 10$ N.
$$F_{c1} = \frac{(15)(2) + (3)(10)}{3+2} = \frac{30 + 30}{5} = \frac{60}{5} = 12 \text{ N}$$[Q2] Configuration (b)
The positions of the blocks are swapped. The acceleration of the system remains the same, as the total mass and net external force are unchanged.
$$a = \frac{F-f}{M+m}$$Let the new contact force be $F_{c2}$. We analyze the forces on block $m$. The forces are the applied force $F$ to the right and the contact force from block $M$, $F_{c2}$, to the left. Applying Newton's second law to block $m$:
$$F - F_{c2} = ma$$Solving for the contact force $F_{c2}$:
$$F_{c2} = F - ma$$Substituting the expression for acceleration $a$:
$$F_{c2} = F - m\left(\frac{F-f}{M+m}\right) = \frac{F(M+m) - m(F-f)}{M+m}$$ $$F_{c2} = \frac{FM + Fm - mF + mf}{M+m} = \frac{FM + mf}{M+m}$$Substituting the given values:
$$F_{c2} = \frac{(15)(3) + (10)(2)}{3+2} = \frac{45 + 20}{5} = \frac{65}{5} = 13 \text{ N}$$