Source: Principles of Physics
Problem
Two blocks of mass $m$ and $M$ are in contact on a frictionless horizontal surface. A horizontal force $\vec{F}$ is applied to the smaller block of mass $m$. The coefficient of static friction between the blocks is $\mu_s$.
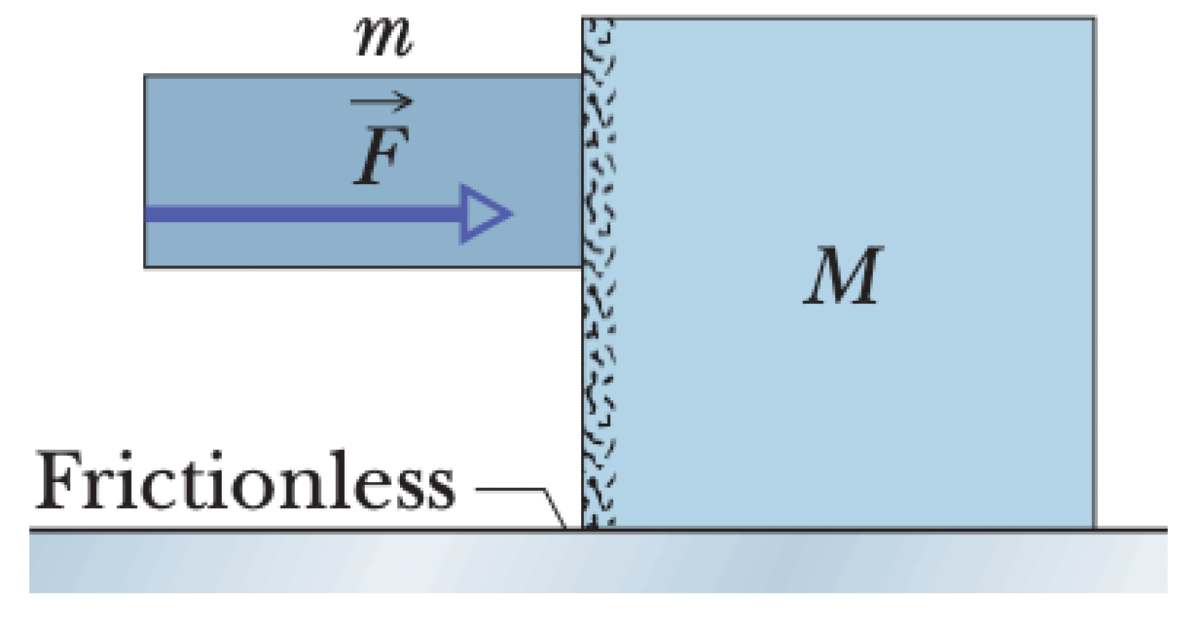
P0411-problem-1
For block $m$ to remain stationary vertically, the upward static friction $f_s$ must balance its weight $mg$. The minimum required force $F_{min}$ corresponds to the maximum static friction, $f_{s,max} = \mu_s N$, where $N$ is the normal force between the blocks.
From vertical equilibrium on block $m$:
$$f_{s,max} = mg \implies \mu_s N = mg$$ $$N = \frac{mg}{\mu_s}$$The normal force $N$ is the only horizontal force acting on block $M$, causing both blocks to accelerate together with acceleration $a$:
$$N = Ma \implies a = \frac{N}{M} = \frac{mg}{\mu_s M}$$The external force $F$ must accelerate the total mass of the system $(M+m)$ at this rate:
$$F = (M+m)a$$Substituting the expression for $a$ gives the minimum force:
$$F_{min} = (M+m)\left(\frac{mg}{\mu_s M}\right)$$