Source: Physics Olympiad Course book
Problem Sets:
Problem
A small ball is launched horizontally from the top of a building with an initial speed of $v_0 = 10$ m/s. Air resistance is negligible. At a certain point in its trajectory, the magnitude of the ball's normal acceleration is $a_n = 5$ m/s².
- Find the vertical distance the ball has fallen to reach this point.
- Find the radius of curvature of the trajectory at this point.
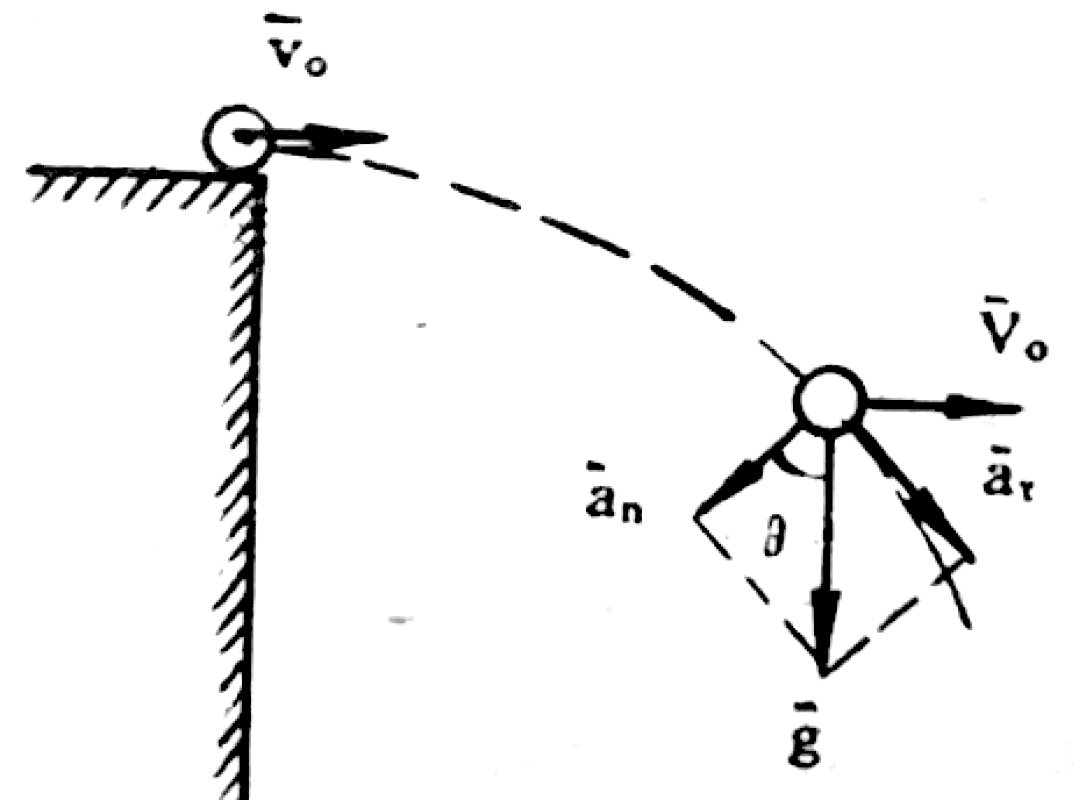
01K4QQ9GZ29H4VNB8REFQBHN6A
[Q1] The vertical distance the ball has fallen is:
$$y = \frac{v_0^2}{2g} \left[ \left(\frac{g}{a_n}\right)^2 - 1 \right] = 15 \text{ m}$$[Q2] The radius of curvature of the trajectory is:
$$\rho = \frac{g^2 v_0^2}{a_n^3} = 80 \text{ m}$$The projectile's velocity components are $v_x = v_0$ and $v_y = gt$. The speed is $v = \sqrt{v_0^2 + v_y^2}$. The only acceleration is gravity, $\vec{a} = \vec{g}$, acting vertically downwards.
The total acceleration can be decomposed into normal ($a_n$) and tangential ($a_t$) components. The normal acceleration is the component of $\vec{g}$ perpendicular to the velocity vector $\vec{v}$. If $\theta$ is the angle of $\vec{v}$ below the horizontal, then:
$$a_n = g \cos\theta$$From the velocity components, we also have:
$$\cos\theta = \frac{v_x}{v} = \frac{v_0}{\sqrt{v_0^2 + v_y^2}}$$Combining these two relations gives:
$$a_n = g \frac{v_0}{\sqrt{v_0^2 + v_y^2}}$$[Q1] Find the vertical distance the ball has fallen to reach this point. First, we solve the expression above for the vertical velocity component $v_y$.
$$v_0^2 + v_y^2 = \left(\frac{g v_0}{a_n}\right)^2$$ $$v_y^2 = v_0^2 \left[ \left(\frac{g}{a_n}\right)^2 - 1 \right]$$The vertical distance fallen, $y$, is related to the vertical velocity by the kinematic equation $v_y^2 = 2gy$ (since $v_{y0}=0$). Equating the expressions for $v_y^2$:
$$2gy = v_0^2 \left[ \left(\frac{g}{a_n}\right)^2 - 1 \right]$$ $$y = \frac{v_0^2}{2g} \left[ \left(\frac{g}{a_n}\right)^2 - 1 \right]$$Given the clean values, we assume $g=10$ m/s². Substituting $v_0 = 10$ m/s and $a_n = 5$ m/s²:
$$y = \frac{(10 \text{ m/s})^2}{2(10 \text{ m/s²})} \left[ \left(\frac{10 \text{ m/s²}}{5 \text{ m/s²}}\right)^2 - 1 \right] = 5(2^2 - 1) = 15 \text{ m}$$[Q2] Find the radius of curvature of the trajectory at this point. The normal acceleration is related to the speed $v$ and radius of curvature $\rho$ by $a_n = v^2/\rho$. Thus, $\rho = v^2/a_n$. The speed squared is $v^2 = v_0^2 + v_y^2$. From our work in Q1:
$$v^2 = \left(\frac{g v_0}{a_n}\right)^2$$Substituting this into the equation for $\rho$:
$$\rho = \frac{1}{a_n} \left(\frac{g v_0}{a_n}\right)^2 = \frac{g^2 v_0^2}{a_n^3}$$Substituting the numerical values:
$$\rho = \frac{(10 \text{ m/s²})^2 (10 \text{ m/s})^2}{(5 \text{ m/s²})^3} = \frac{(100)(100)}{125} = \frac{10000}{125} = 80 \text{ m}$$