Source: Physics Olympiad Course book
Problem Sets:
Problem
As shown in Figure, a wheel with radius $r$ rolls without slipping on the outer surface of a fixed cylinder with radius $R$. The center of the wheel, O, moves with a constant speed $V$.
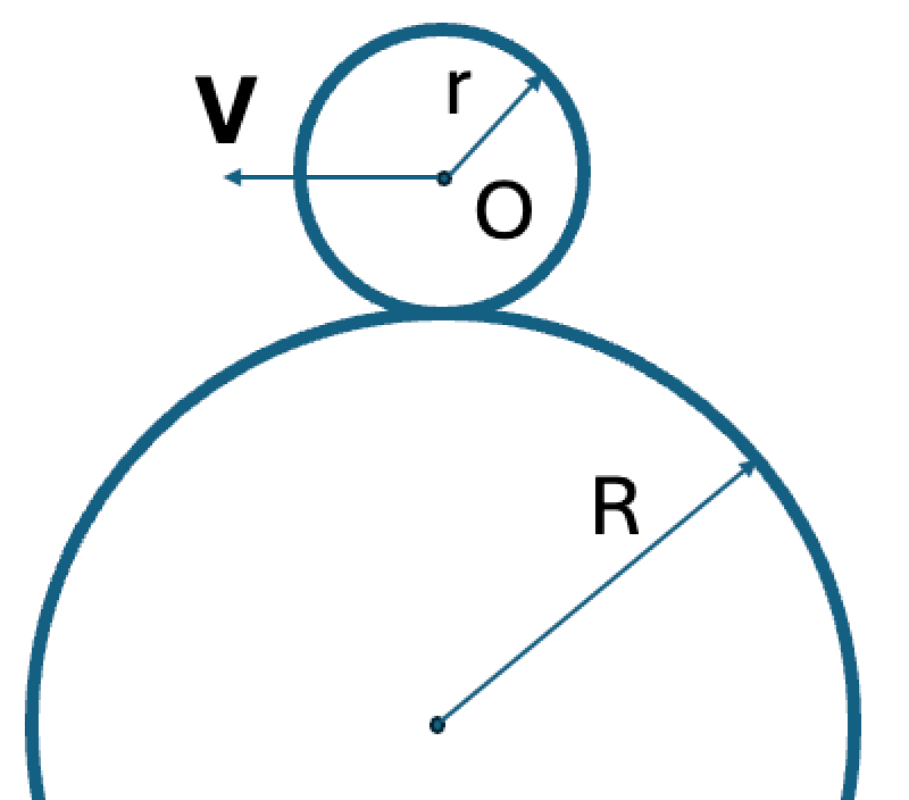
01K4QQ84BGZ2WT39HWR9CCXE8Y
The acceleration of the contact point P on the wheel has a magnitude:
$$a_P = \frac{V^2 R}{r(R+r)}$$The direction is radially outward from the center of the fixed cylinder.
The acceleration of any point P on the wheel can be determined by the principle of relative motion. The acceleration of P is the vector sum of the acceleration of the wheel's center, O, and the acceleration of P relative to O.
$$\vec{a}_P = \vec{a}_O + \vec{a}_{P/O}$$1. Acceleration of the Center of the Wheel ($\vec{a}_O$) The center of the wheel, O, moves along a circular path of radius $(R+r)$ around the center of the fixed cylinder. Since the speed $V$ is constant, the acceleration of O is purely centripetal, directed towards the center of its circular path (i.e., towards the center of the large cylinder). At the position shown, this direction is vertically downward. The magnitude is given by:
$$a_O = \frac{V^2}{R+r}$$2. Acceleration of P relative to O ($\vec{a}_{P/O}$) The point P moves in a circle of radius $r$ relative to the center O. Its acceleration relative to O can have a radial (centripetal) component and a tangential component. The radial component is directed from P towards O (vertically upward) and has a magnitude:
$$a_{P/O, \text{rad}} = \omega^2 r$$where $\omega$ is the angular speed of the wheel.
The tangential component has a magnitude $a_{P/O, \text{tan}} = \alpha r$, where $\alpha$ is the angular acceleration.
3. No-Slipping Condition The "rolling without slipping" condition implies that the instantaneous velocity of the contact point P on the wheel is zero (since the cylinder is fixed). The velocity of P is the sum of the velocity of the center, $\vec{V}$, and the velocity of P relative to O, $\vec{v}_{P/O}$. These two vectors must cancel out.
$$V = v_{P/O} = \omega r$$From this, we find the angular speed:
$$\omega = \frac{V}{r}$$Since $V$ and $r$ are constants, the angular speed $\omega$ is also constant. Therefore, the angular acceleration $\alpha = d\omega/dt = 0$, and the tangential component of the relative acceleration is zero.
$$a_{P/O, \text{tan}} = 0$$Now, we can find the magnitude of the relative radial acceleration:
$$a_{P/O} = a_{P/O, \text{rad}} = \omega^2 r = \left(\frac{V}{r}\right)^2 r = \frac{V^2}{r}$$This acceleration is directed upward, from P to O.
4. Total Acceleration of P The total acceleration of P is the vector sum of $\vec{a}_O$ and $\vec{a}_{P/O}$. Both accelerations are vertical but in opposite directions.
- $\vec{a}_O$: Magnitude $\frac{V^2}{R+r}$, directed downward.
- $\vec{a}_{P/O}$: Magnitude $\frac{V^2}{r}$, directed upward.
Since $r < R+r$, it follows that $\frac{1}{r} > \frac{1}{R+r}$, which means $a_{P/O} > a_O$. The net acceleration is therefore directed upward. The magnitude is:
$$a_P = a_{P/O} - a_O = \frac{V^2}{r} - \frac{V^2}{R+r}$$ $$a_P = V^2 \left(\frac{1}{r} - \frac{1}{R+r}\right)$$Simplifying the expression:
$$a_P = V^2 \left(\frac{(R+r) - r}{r(R+r)}\right) = V^2 \frac{R}{r(R+r)}$$The acceleration of the contact point P is directed vertically upward (radially away from the center of the large cylinder).