Source: Physics Olympiad Course book
Problem Sets:
Problem
As shown in the diagram, a person on a pier of height $h$ above the water pulls a rope attached to a boat at point A. The person pulls the rope, causing it to be reeled in at a constant speed $V$.
- Find the speed of the small boat when the angle between the rope and the water surface is $\theta = 30^{\circ}$.
- Find the acceleration of the small boat when the angle between the rope and the water surface is $\theta = 30^{\circ}$.
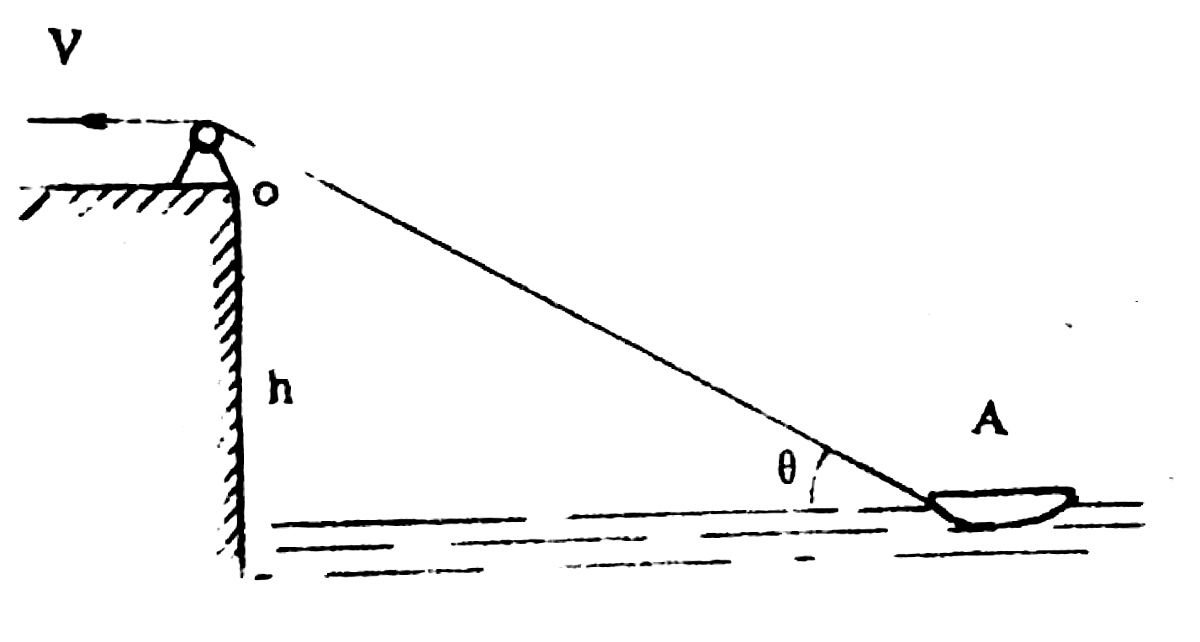
01K4QNY8BKVVJ3MEFHYY308DMF
[Q1] The speed of the small boat is given by the formula:
$$v_b = \frac{V}{\cos\theta}$$At $\theta = 30^{\circ}$, the speed is:
$$v_b = \frac{2V}{\sqrt{3}}$$[Q2] The acceleration of the small boat is given by the formula:
$$a_b = \frac{V^2}{h}\tan^3\theta$$At $\theta = 30^{\circ}$, the acceleration is:
$$a_b = \frac{\sqrt{3}V^2}{9h}$$Let the horizontal distance from the pier to the boat be $x$, and the length of the rope be $l$. The pier has a constant height $h$. From the right-angled triangle in the diagram, we have the following geometric relationships:
$$l^2 = x^2 + h^2$$ $$x = l \cos\theta \quad \text{and} \quad h = l \sin\theta$$The rope is reeled in at a constant speed $V$, meaning the rate of change of the rope's length is $\frac{dl}{dt} = -V$. The boat's velocity is $\vec{v}_b$ (purely horizontal) and its speed is $v_b = |\vec{v}_b|$. The boat's acceleration is $\vec{a}_b$.
[Q1] Speed of the Small Boat
We can find the boat's speed by relating it to the speed of the rope. The speed $V$ at which the rope is pulled in is equal to the component of the boat's velocity $\vec{v}_b$ along the direction of the rope.
From the geometry, the component of $v_b$ along the rope is $v_b \cos\theta$.
$$V = v_b \cos\theta$$Solving for the speed of the boat, $v_b$:
$$v_b = \frac{V}{\cos\theta}$$For $\theta = 30^{\circ}$:
$$v_b = \frac{V}{\cos 30^{\circ}} = \frac{V}{\sqrt{3}/2} = \frac{2V}{\sqrt{3}}$$[Q2] Acceleration of the Small Boat
To find the acceleration, we can differentiate the kinematic relationships with respect to time. Let $v_x$ be the velocity component of the boat along the x-axis (towards the pier, so $v_x = -v_b$). Let $a_x$ be the acceleration component.
The relation between the length rates is found by differentiating $l^2 = x^2 + h^2$:
$$2l \frac{dl}{dt} = 2x \frac{dx}{dt} \implies l(-V) = x v_x$$Differentiating this velocity constraint equation with respect to time:
$$\frac{d}{dt}(l(-V)) = \frac{d}{dt}(x v_x)$$ $$\frac{dl}{dt}(-V) + l \frac{d(-V)}{dt} = \frac{dx}{dt}v_x + x\frac{dv_x}{dt}$$Since $V$ is constant, $\frac{d(-V)}{dt}=0$. Substituting $\frac{dl}{dt}=-V$, $\frac{dx}{dt}=v_x$, and $\frac{dv_x}{dt}=a_x$:
$$(-V)(-V) = v_x^2 + x a_x$$ $$V^2 = v_x^2 + x a_x$$Solving for the acceleration $a_x$:
$$a_x = \frac{V^2 - v_x^2}{x}$$From Q1, the boat's speed is $v_b = V/\cos\theta$. So, $v_x = -v_b = -V/\cos\theta$. We also know $x=h/\tan\theta$. Substituting these into the expression for $a_x$:
$$a_x = \frac{V^2 - (-V/\cos\theta)^2}{h/\tan\theta} = \frac{V^2(1 - \sec^2\theta)}{h/\tan\theta}$$Using the trigonometric identity $1 - \sec^2\theta = -\tan^2\theta$:
$$a_x = \frac{V^2(-\tan^2\theta)}{h/\tan\theta} = -\frac{V^2}{h}\tan^3\theta$$The acceleration is directed towards the pier. The magnitude of the acceleration is $a_b = |a_x|$:
$$a_b = \frac{V^2}{h}\tan^3\theta$$For $\theta = 30^{\circ}$:
$$a_b = \frac{V^2}{h}(\tan 30^{\circ})^3 = \frac{V^2}{h}\left(\frac{1}{\sqrt{3}}\right)^3 = \frac{V^2}{3\sqrt{3}h} = \frac{\sqrt{3}V^2}{9h}$$