Source: Physics Competition - Mechanics
Problem Sets:
Problem
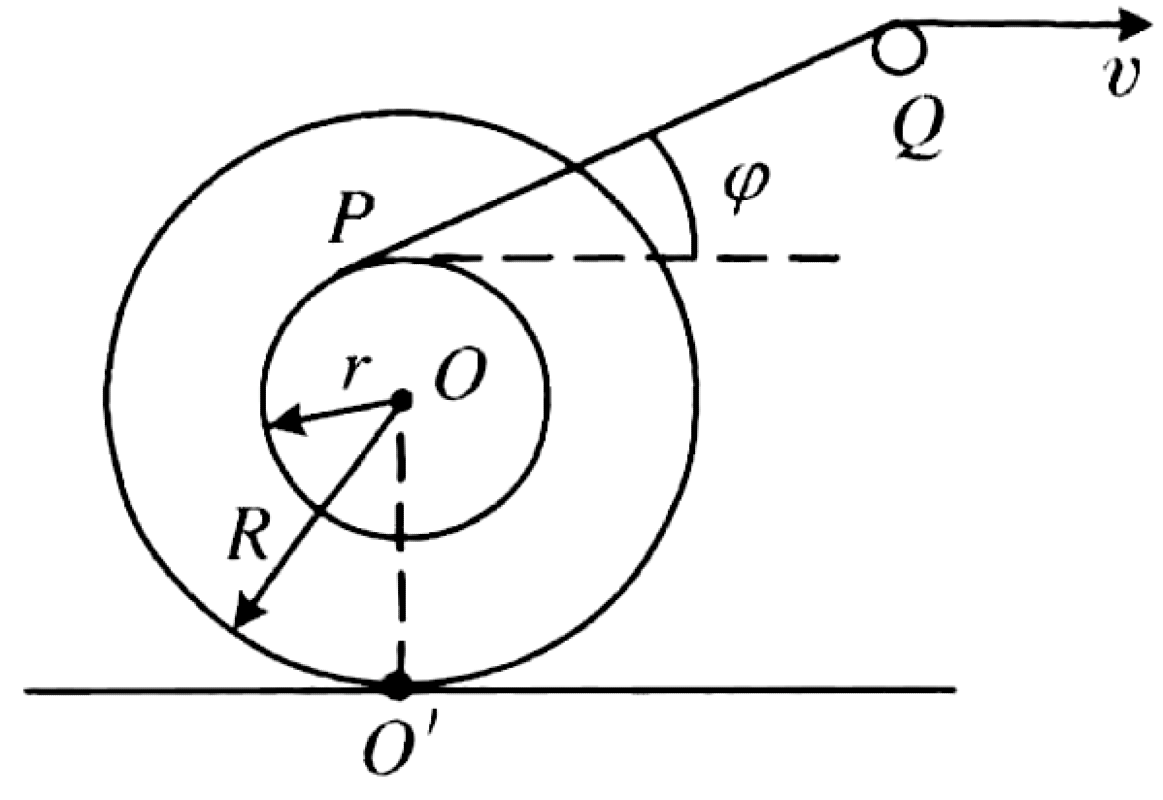
A spool is formed by a small cylinder of radius $r$ coaxially fixed to a large cylinder of radius $R$. A string is wound on the inner cylinder. The string is drawn out, passes over a pulley Q, and its end is pulled with a constant velocity $v$. Simultaneously, the spool rolls without slipping on a horizontal surface. The segment of the string from the spool to the pulley, PQ, makes an angle $\varphi$ with the horizontal, as shown in the diagram.
01K4H1BRVRXNRG7M9N4VQEKVTH
The speed of the spool's center, O, is given by:
$$v_O = \frac{vR}{R\cos\varphi + r}$$To determine the speed of the spool's center, v_O, we will relate it to the given speed v of the string by analyzing the spool's kinematics.
-
Rolling Without Slipping Condition: The spool rolls without slipping on the horizontal surface. This means the point of contact
$$v_O = \omega R$$O'is instantaneously at rest. This condition relates the speed of the center,v_O, to the angular speed\omegaof the spool: -
Velocity of the Unwinding Point P: The velocity of point
$$\vec{r}_{OP} = r\cos(90^\circ+\varphi)\hat{i} + r\sin(90^\circ+\varphi)\hat{j} = -r\sin\varphi\,\hat{i} + r\cos\varphi\,\hat{j}$$Pon the inner cylinder, where the string unwinds, is the vector sum of the translational velocity of the centerO(\vec{v}_O) and the rotational velocity ofPaboutO(\vec{v}_{P/O} = \vec{\omega} \times \vec{r}_{OP}). Let's define a coordinate system with\hat{i}pointing horizontally to the right and\hat{j}vertically upwards. The velocity of the center is\vec{v}_O = v_O \hat{i}. For the spool to roll to the right, the angular velocity must be clockwise, so\vec{\omega} = -\omega \hat{k}. The string segmentPQis tangent to the inner cylinder atP. Thus, the radiusOPis perpendicular toPQ. AsPQmakes an angle\varphiwith the horizontal, the position vector\vec{r}_{OP}makes an angle of90^\circ + \varphiwith the\hat{i}axis.The velocity of
$$\vec{v}_P = \vec{v}_O + \vec{\omega} \times \vec{r}_{OP} = v_O \hat{i} + (-\omega \hat{k}) \times (-r\sin\varphi\,\hat{i} + r\cos\varphi\,\hat{j})$$ $$\vec{v}_P = v_O \hat{i} + \omega r\sin\varphi\,(\hat{k}\times\hat{i}) - \omega r\cos\varphi\,(\hat{k}\times\hat{j})$$Pis then:Using
$$\vec{v}_P = v_O \hat{i} + \omega r\sin\varphi\,\hat{j} + \omega r\cos\varphi\,\hat{i}$$ $$\vec{v}_P = (v_O + \omega r\cos\varphi)\hat{i} + (\omega r\sin\varphi)\hat{j}$$\hat{k}\times\hat{i} = \hat{j}and\hat{k}\times\hat{j} = -\hat{i}: -
String Constraint: The string is inextensible and is pulled with a speed
$$v = \vec{v}_P \cdot \hat{u}_{PQ}$$ $$v = (v_O + \omega r\cos\varphi)\cos\varphi + (\omega r\sin\varphi)\sin\varphi$$ $$v = v_O\cos\varphi + \omega r(\cos^2\varphi + \sin^2\varphi)$$ $$v = v_O\cos\varphi + \omega r$$v. This means the component of\vec{v}_Palong the direction of the string must be equal tov. The unit vector along the stringPQis\hat{u}_{PQ} = \cos\varphi\,\hat{i} + \sin\varphi\,\hat{j}. -
Solving for the Speed of the Center
v_O: We now have a system of two equations:- $v_O = \omega R$
- $v = v_O\cos\varphi + \omega r$
From equation (1), we express
$$v = v_O\cos\varphi + \left(\frac{v_O}{R}\right)r$$\omegain terms ofv_O:\omega = v_O / R. Substituting this into equation (2):Factor out
$$v = v_O \left(\cos\varphi + \frac{r}{R}\right)$$v_O:Finally, solving for
$$v_O = \frac{v}{\cos\varphi + \frac{r}{R}} = \frac{vR}{R\cos\varphi + r}$$v_O: