Source: Physics Competition - Mechanics
Problem Sets:
Problem
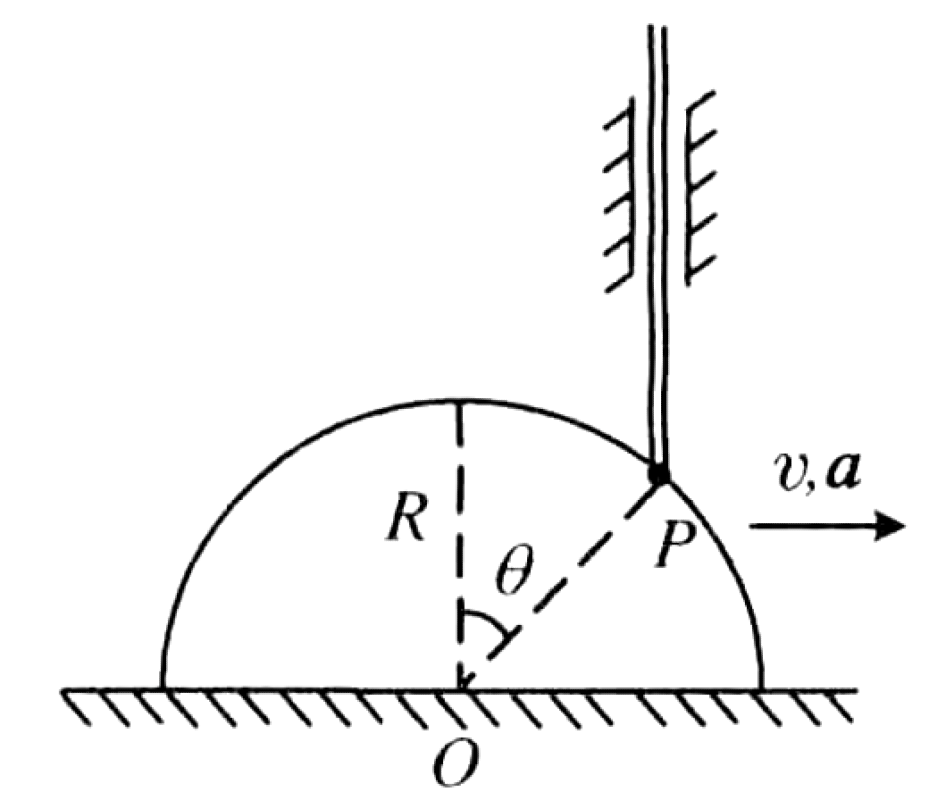
As shown in the figure, a semi-cylinder with radius R undergoes uniformly accelerated motion with a constant horizontal acceleration $a$. A vertical rod, constrained to move only in the vertical direction, rests on the curved surface of the semi-cylinder. At the instant when the semi-cylinder's horizontal velocity is $v$, the contact point P between the rod and the semi-cylinder is at an angular position $\theta$ with respect to the vertical axis.
- Find the velocity of the vertical rod at this instant.
- Find the acceleration of the vertical rod at this instant.
01K4HDTB2H2DQKMGWWZJQEYEZ1
[Q1] The velocity of the vertical rod is:
$$ v_y = v \tan\theta $$[Q2] The acceleration of the vertical rod is:
$$ a_y = a\tan\theta - \frac{v^2}{R\cos^3\theta} $$The kinematics of the system is governed by the geometric constraint that the vertical rod remains in contact with the moving semi-cylinder. Let's establish a coordinate system with the origin at the center of the semi-cylinder's base, O, at the instant shown. The horizontal position of the rod is fixed, while the semi-cylinder moves horizontally.
The position of the contact point P is described by its vertical height $y_P$ and the angle $\theta$. The motion of the semi-cylinder is described by its horizontal velocity $v$ and acceleration $a$.
Q1: Velocity of the vertical rod
We relate the velocity of the rod to the velocity of the semi-cylinder using the no-penetration constraint at the contact point P. The rod is constrained to move vertically, and the semi-cylinder moves horizontally.
-
Velocities at the contact point P: The velocity of the rod at P is purely vertical:
$$ \vec{v}_{rod} = v_y \hat{j} $$The velocity of the material point on the semi-cylinder at P is purely horizontal (as it's part of a translating rigid body):
$$ \vec{v}_{cyl} = v \hat{i} $$ -
No-penetration condition: For the rod and semi-cylinder to remain in contact without penetrating each other, the component of their relative velocity along the normal to the surface must be zero. The normal vector $\vec{n}$ at point P is directed from O to P, making an angle $\theta$ with the vertical.
$$ \vec{n} = \sin\theta \hat{i} + \cos\theta \hat{j} $$The condition is $(\vec{v}_{rod} - \vec{v}_{cyl}) \cdot \vec{n} = 0$, which simplifies to:
$$ \vec{v}_{rod} \cdot \vec{n} = \vec{v}_{cyl} \cdot \vec{n} $$ -
Derivation: Substituting the velocity and normal vectors:
$$ (v_y \hat{j}) \cdot (\sin\theta \hat{i} + \cos\theta \hat{j}) = (v \hat{i}) \cdot (\sin\theta \hat{i} + \cos\theta \hat{j}) $$ $$ v_y \cos\theta = v \sin\theta $$Solving for the rod's velocity $v_y$:
$$ v_y = v \frac{\sin\theta}{\cos\theta} = v \tan\theta $$
Q2: Acceleration of the vertical rod
To find the acceleration of the rod, $a_y$, we differentiate its velocity $v_y$ with respect to time. This requires knowing the rate of change of the angle, $\dot{\theta}$.
-
Geometric Constraint: Let the horizontal position of the semi-cylinder's center be $x_O(t)$ and the fixed horizontal position of the rod be $x_P$. The geometric relationship is:
$$ x_P = x_O(t) + R \sin\theta $$Differentiating with respect to time, noting that $x_P$ is constant ($\dot{x}_P=0$) and $\dot{x}_O = v$:
$$ 0 = v + R\cos\theta \cdot \frac{d\theta}{dt} \implies \dot{\theta} = -\frac{v}{R\cos\theta} $$ -
Derivation of Acceleration: Now, differentiate the velocity expression $v_y = v \tan\theta$ with respect to time using the product rule and chain rule:
$$ a_y = \frac{dv_y}{dt} = \frac{d}{dt}(v \tan\theta) = \frac{dv}{dt}\tan\theta + v \frac{d}{dt}(\tan\theta) $$We are given $\frac{dv}{dt} = a$. The derivative of $\tan\theta$ is:
$$ \frac{d}{dt}(\tan\theta) = \frac{d(\tan\theta)}{d\theta} \frac{d\theta}{dt} = \sec^2\theta \cdot \dot{\theta} $$Substituting this and the expression for $\dot{\theta}$:
$$ a_y = a\tan\theta + v (\sec^2\theta) \left(-\frac{v}{R\cos\theta}\right) $$ $$ a_y = a\tan\theta - \frac{v^2}{R} \frac{1}{\cos^2\theta} \frac{1}{\cos\theta} $$Simplifying gives the final expression for the rod's acceleration:
$$ a_y = a\tan\theta - \frac{v^2}{R\cos^3\theta} $$