Source: Physics Competition - Mechanics
Problem Sets:
Problem
As shown in the figure, one end of a thin rope is fixed at point A. A weight B is attached to the rope at a distance $a$ from A, making the length of segment AB constant, $l_{AB} = a$. The other end of the rope passes over a fixed pulley at point C. Points A and C lie on the same horizontal line. The free end of the rope is pulled with a constant speed $v$. At the instant shown, the rope segments AB and BC make angles $\alpha$ and $\beta$ with the horizontal, respectively.
- Find the velocity of point B, $\vec{v}_B$.
- Find the acceleration of point B along the direction of AB, $a_{B, AB}$.
- Find the acceleration of point B along the direction of BC, $a_{B, BC}$.
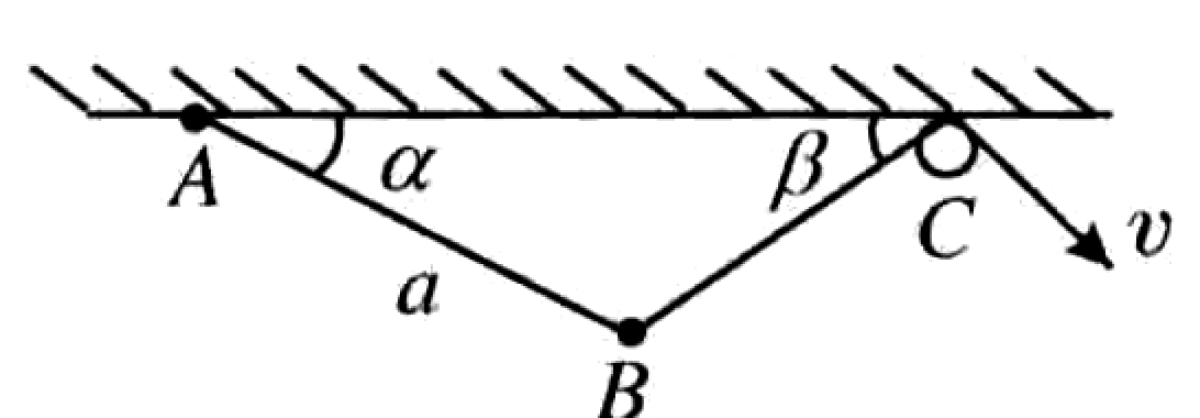
01K4JFYEKW9VQA5RPZ11Z0641B
[Q1] The velocity of point B, $\vec{v}_B$, has magnitude $v_B = \frac{v}{\sin(\alpha+\beta)}$ and is directed perpendicularly to the segment AB.
[Q2] The acceleration of point B along the direction of AB is:
$$a_{B, AB} = -\frac{v^2}{a \sin^2(\alpha+\beta)}$$[Q3] The acceleration of point B along the direction of BC is:
$$a_{B, BC} = \frac{v^2 \sin\beta \cos^2(\alpha+\beta)}{a \sin\alpha \sin^2(\alpha+\beta)}$$[Q1] Find the velocity of point B, $\vec{v}_B$.
The motion of point B is governed by two constraints:
- Fixed length of AB: Since point A is fixed and the length $l_{AB} = a$ is constant, point B must move in a circle of radius $a$ around A. This implies that the velocity vector $\vec{v}_B$ is perpendicular to the rope segment AB.
- Inextensible rope over pulley: The free end of the rope is pulled with a constant speed $v$. This means the length of the rope segment BC is decreasing at a rate of $v$. The rate of change of length $l_{BC}$ is the projection of $\vec{v}_B$ onto the direction of BC. Therefore, the component of $\vec{v}_B$ along the direction from B to C is $v$.
Let $v_B$ be the magnitude of the velocity $\vec{v}_B$. Let's determine the angle between the vector $\vec{v}_B$ and the segment BC.
- The direction of $\vec{v}_B$ is perpendicular to AB.
- The angle between the segments AB and BC is $\alpha + \beta$.
- The angle $\phi$ between $\vec{v}_B$ and BC is therefore $|\frac{\pi}{2} - (\alpha+\beta)|$.
The projection of $\vec{v}_B$ onto BC is $v_B \cos\phi = v$.
$$v_B \cos\left(\frac{\pi}{2} - (\alpha+\beta)\right) = v$$ $$v_B \sin(\alpha+\beta) = v$$Solving for the magnitude $v_B$:
$$v_B = \frac{v}{\sin(\alpha+\beta)}$$The velocity vector $\vec{v}_B$ has this magnitude and a direction perpendicular to AB, pointing towards the line AC.
[Q2] Find the acceleration of point B along the direction of AB, $a_{B, AB}$.
Since point B moves in a circular path of radius $a$ around the fixed point A, it has a radial (centripetal) acceleration directed towards the center A. The magnitude of this acceleration is given by:
$$a_{rad} = \frac{v_B^2}{a}$$The question asks for the acceleration component along the direction of AB (from A to B). This is opposite to the direction of the centripetal acceleration (from B to A).
$$a_{B, AB} = -a_{rad} = -\frac{v_B^2}{a}$$Substituting the expression for $v_B$ from Q1:
$$a_{B, AB} = -\frac{1}{a} \left( \frac{v}{\sin(\alpha+\beta)} \right)^2 = -\frac{v^2}{a \sin^2(\alpha+\beta)}$$[Q3] Find the acceleration of point B along the direction of BC, $a_{B, BC}$.
We consider the motion of B relative to the fixed point C. The acceleration component along BC is the radial component of acceleration in a polar coordinate system centered at C. The general expression for radial acceleration is $a_r = \ddot{r} - r\dot{\theta}^2$.
- The radial distance is $r = l_{BC}$. Its rate of change is $\dot{l}_{BC} = -v$ (since the rope is pulled in). As $v$ is constant, the second derivative is $\ddot{l}_{BC} = 0$.
- The angular velocity is $\dot{\theta} = \omega_{BC}$. The term $-r\dot{\theta}^2$ is the centripetal acceleration, directed towards C.
The acceleration component along the direction CB (towards C) is $\ddot{l}_{BC} - l_{BC}\omega_{BC}^2 = 0 - l_{BC}\omega_{BC}^2$. The component along BC (away from C) is the negative of this:
$$a_{B, BC} = l_{BC}\omega_{BC}^2$$The angular velocity $\omega_{BC}$ is related to the component of B's velocity perpendicular to BC, $v_{B, \perp BC}$: $\omega_{BC} = \frac{v_{B, \perp BC}}{l_{BC}}$. Substituting this gives:
$$a_{B, BC} = l_{BC} \left( \frac{v_{B, \perp BC}}{l_{BC}} \right)^2 = \frac{v_{B, \perp BC}^2}{l_{BC}}$$Now, we find $v_{B, \perp BC}$ and $l_{BC}$:
- $v_{B, \perp BC}$ is the component of $\vec{v}_B$ perpendicular to BC.
Substituting $v_B = \frac{v}{\sin(\alpha+\beta)}$:
$$v_{B, \perp BC} = \frac{v \cos(\alpha+\beta)}{\sin(\alpha+\beta)} = v \cot(\alpha+\beta)$$- $l_{BC}$ is found using the Law of Sines in triangle ABC:
Finally, we substitute these into the expression for $a_{B, BC}$:
$$a_{B, BC} = \frac{(v \cot(\alpha+\beta))^2}{a \sin\alpha / \sin\beta} = \frac{v^2 \cot^2(\alpha+\beta) \sin\beta}{a \sin\alpha}$$ $$a_{B, BC} = \frac{v^2 \sin\beta \cos^2(\alpha+\beta)}{a \sin\alpha \sin^2(\alpha+\beta)}$$