Source: Physics Competition - Mechanics
Problem Sets:
Problem
In a plane, two straight lines, AB and CD, intersect at an angle $\phi$. The line AB moves with a velocity $v_1$ in a direction perpendicular to itself. The line CD moves with a velocity $v_2$ in a direction perpendicular to itself. The intersection of the two lines is point P.
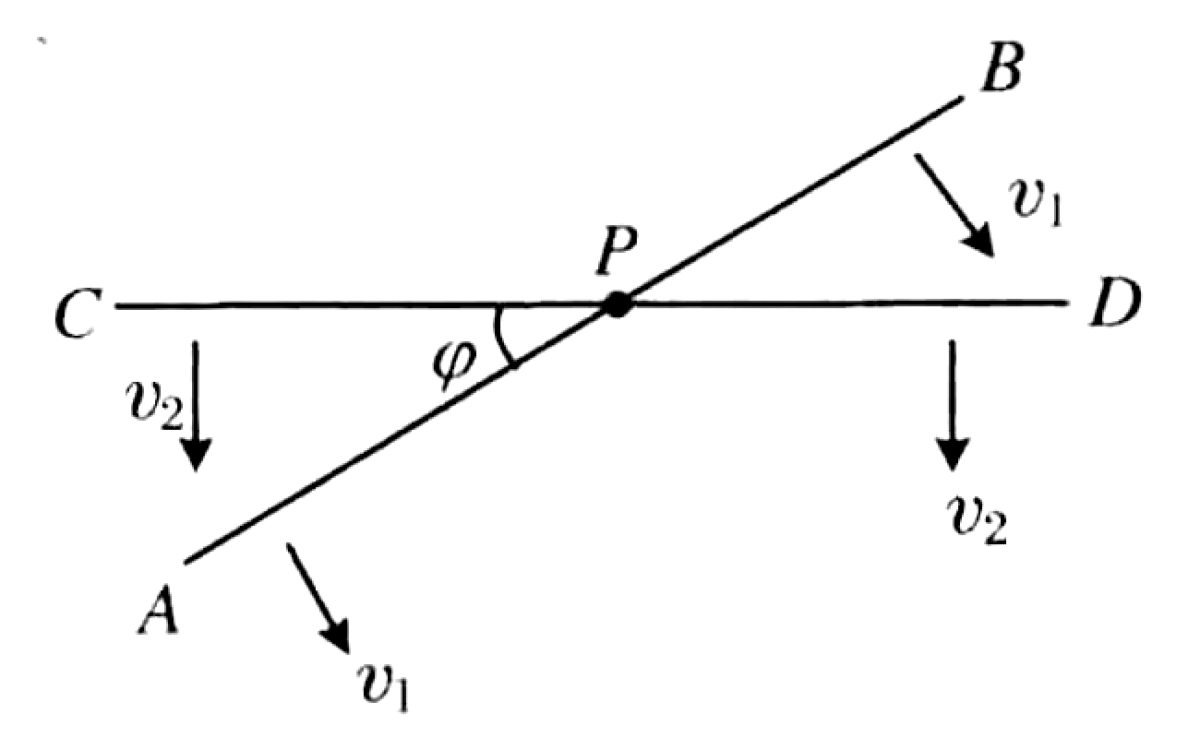
01K4JGE4YSG30E2912R07XY9AB
The magnitude of the velocity of the intersection point P is:
$$ v_P = \frac{\sqrt{v_1^2 + v_2^2 - 2v_1 v_2 \cos\phi}}{\sin\phi} $$The velocity of the intersection point P, denoted by $\vec{v}_P$, must satisfy the kinematic constraints imposed by the two moving lines. Specifically, the component of $\vec{v}_P$ perpendicular to each line must be equal to the velocity of that line.
Let's establish a coordinate system with the origin at the intersection point P at a given instant. We align the x-axis with the line CD, and the y-axis perpendicular to it.
-
Constraint from line CD: The line CD moves with velocity $v_2$ in a direction perpendicular to itself. As per the diagram, this velocity is in the negative y-direction. Let $\hat{n}_2$ be the unit normal vector for this motion, so $\hat{n}_2 = (0, -1)$. The velocity of line CD is $\vec{v}_{L2} = v_2 \hat{n}_2$. The component of $\vec{v}_P$ along $\hat{n}_2$ must be $v_2$. Let $\vec{v}_P = (v_{Px}, v_{Py})$.
$$ \vec{v}_P \cdot \hat{n}_2 = v_2 $$ $$ (v_{Px}, v_{Py}) \cdot (0, -1) = v_2 $$ $$ -v_{Py} = v_2 \implies v_{Py} = -v_2 $$ -
Constraint from line AB: The line AB makes an angle $\phi$ with line CD (the x-axis). The unit vector tangent to AB is $\hat{t}_1 = (\cos\phi, \sin\phi)$. The unit normal vector $\hat{n}_1$ must be perpendicular to $\hat{t}_1$. From the diagram, the velocity $\vec{v}_1$ is directed "down and to the right", so we choose the normal vector $\hat{n}_1 = (\sin\phi, -\cos\phi)$. The velocity of line AB is $\vec{v}_{L1} = v_1 \hat{n}_1$. The component of $\vec{v}_P$ along $\hat{n}_1$ must be $v_1$.
$$ \vec{v}_P \cdot \hat{n}_1 = v_1 $$ $$ (v_{Px}, v_{Py}) \cdot (\sin\phi, -\cos\phi) = v_1 $$ $$ v_{Px} \sin\phi - v_{Py} \cos\phi = v_1 $$ -
Solving for the components of $\vec{v}_P$: Substitute $v_{Py} = -v_2$ into the second constraint equation:
$$ v_{Px} \sin\phi - (-v_2) \cos\phi = v_1 $$ $$ v_{Px} \sin\phi + v_2 \cos\phi = v_1 $$Solving for $v_{Px}$:
$$ v_{Px} = \frac{v_1 - v_2 \cos\phi}{\sin\phi} $$ -
Finding the magnitude of $\vec{v}_P$: The magnitude of the velocity of the intersection point, $v_P$, is given by $v_P = \sqrt{v_{Px}^2 + v_{Py}^2}$.
$$ v_P^2 = \left(\frac{v_1 - v_2 \cos\phi}{\sin\phi}\right)^2 + (-v_2)^2 $$ $$ v_P^2 = \frac{v_1^2 - 2v_1 v_2 \cos\phi + v_2^2 \cos^2\phi}{\sin^2\phi} + v_2^2 $$ $$ v_P^2 = \frac{v_1^2 - 2v_1 v_2 \cos\phi + v_2^2 \cos^2\phi + v_2^2 \sin^2\phi}{\sin^2\phi} $$Using the identity $\cos^2\phi + \sin^2\phi = 1$:
$$ v_P^2 = \frac{v_1^2 + v_2^2 - 2v_1 v_2 \cos\phi}{\sin^2\phi} $$Taking the square root gives the magnitude of the velocity:
$$ v_P = \frac{\sqrt{v_1^2 + v_2^2 - 2v_1 v_2 \cos\phi}}{|\sin\phi|} $$Since $\phi$ is the angle between the lines, we typically have $0 < \phi < \pi$, so $\sin\phi > 0$.