Source: Physics Competition - Mechanics
Problem Sets:
Problem
A rigid ring with radius $R$ undergoes pure rolling on a rigid horizontal surface. The center of the ring moves forward horizontally with a constant velocity $v_0$. Consider a point P on the ring that is at the same height as the center.
- Find the instantaneous velocity of point P.
- Find the tangential acceleration of point P.
- Find the normal acceleration of point P.
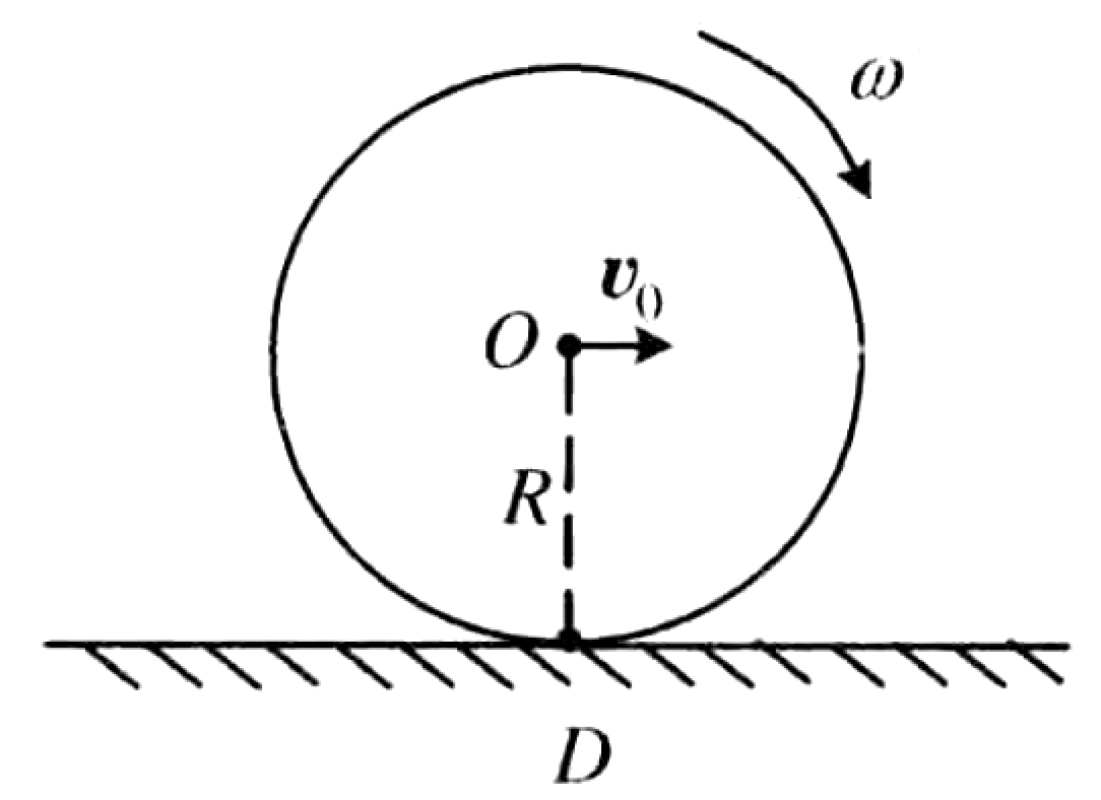
01K4JGKNK8P0HJK6GXXJW4YBX3
[Q1] The instantaneous velocity of point P is:
$$\vec{v}_P = v_0 (\hat{\imath} - \hat{\jmath})$$[Q2] The tangential acceleration of point P is:
$$\vec{a}_{P,t} = -\frac{v_0^2}{2R}(\hat{\imath} - \hat{\jmath})$$[Q3] The normal acceleration of point P is:
$$\vec{a}_{P,n} = -\frac{v_0^2}{2R}(\hat{\imath} + \hat{\jmath})$$The motion of any point on the rolling ring can be described as a superposition of the translational motion of the center O and rotational motion about O. Let's define a coordinate system with the origin on the horizontal surface, $\hat{\imath}$ pointing horizontally to the right, and $\hat{\jmath}$ pointing vertically upwards.
The center of the ring O has velocity $\vec{v}_O = v_0 \hat{\imath}$. Since $v_0$ is constant, the acceleration of the center is $\vec{a}_O = \vec{0}$.
For pure rolling, the velocity of the center $v_0$ and the angular velocity $\omega$ are related by $v_0 = \omega R$. For the ring to move forward, the rotation must be clockwise, so the angular velocity vector is $\vec{\omega} = -\omega \hat{k} = -\frac{v_0}{R} \hat{k}$. Since $v_0$ is constant, the angular acceleration $\vec{\alpha} = \vec{0}$.
We consider the point P at the same height as the center. Let's choose P to be at the front of the ring. The position vector of P relative to O is $\vec{r}_{PO} = R \hat{\imath}$.
[Q1] Instantaneous velocity of point P The velocity of P is the vector sum of the velocity of the center and the velocity of P relative to the center.
$$\vec{v}_P = \vec{v}_O + \vec{v}_{PO} = \vec{v}_O + \vec{\omega} \times \vec{r}_{PO}$$Substituting the known quantities:
$$\vec{v}_{PO} = \left(-\frac{v_0}{R} \hat{k}\right) \times (R \hat{\imath}) = -v_0 (\hat{k} \times \hat{\imath}) = -v_0 \hat{\jmath}$$Thus, the total velocity of P is:
$$\vec{v}_P = v_0 \hat{\imath} - v_0 \hat{\jmath}$$The magnitude of the velocity is $|\vec{v}_P| = \sqrt{v_0^2 + (-v_0)^2} = v_0\sqrt{2}$.
[Q2] & [Q3] Tangential and Normal Acceleration of point P First, we find the total acceleration of P.
$$\vec{a}_P = \vec{a}_O + \vec{a}_{PO} = \vec{a}_O + \vec{\alpha} \times \vec{r}_{PO} + \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PO})$$Since $\vec{a}_O = \vec{0}$ and $\vec{\alpha} = \vec{0}$:
$$\vec{a}_P = \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PO}) = \vec{\omega} \times \vec{v}_{PO}$$ $$\vec{a}_P = \left(-\frac{v_0}{R} \hat{k}\right) \times (-v_0 \hat{\jmath}) = \frac{v_0^2}{R} (\hat{k} \times \hat{\jmath}) = -\frac{v_0^2}{R} \hat{\imath}$$This total acceleration is the centripetal acceleration of P relative to O.
The tangential and normal components of acceleration are projections of the total acceleration $\vec{a}_P$ onto directions parallel and perpendicular to the velocity vector $\vec{v}_P$. The unit vector in the direction of velocity is:
$$\hat{u}_t = \frac{\vec{v}_P}{|\vec{v}_P|} = \frac{v_0 \hat{\imath} - v_0 \hat{\jmath}}{v_0\sqrt{2}} = \frac{1}{\sqrt{2}}(\hat{\imath} - \hat{\jmath})$$Tangential Acceleration [Q2] The tangential acceleration vector is the projection of $\vec{a}_P$ onto $\hat{u}_t$.
$$a_{P,t} = \vec{a}_P \cdot \hat{u}_t = \left(-\frac{v_0^2}{R} \hat{\imath}\right) \cdot \left(\frac{1}{\sqrt{2}}(\hat{\imath} - \hat{\jmath})\right) = -\frac{v_0^2}{R\sqrt{2}}$$ $$\vec{a}_{P,t} = a_{P,t} \hat{u}_t = \left(-\frac{v_0^2}{R\sqrt{2}}\right) \frac{1}{\sqrt{2}}(\hat{\imath} - \hat{\jmath}) = -\frac{v_0^2}{2R}(\hat{\imath} - \hat{\jmath})$$Normal Acceleration [Q3] The normal acceleration vector is the remaining component of the total acceleration.
$$\vec{a}_{P,n} = \vec{a}_P - \vec{a}_{P,t}$$ $$\vec{a}_{P,n} = \left(-\frac{v_0^2}{R} \hat{\imath}\right) - \left(-\frac{v_0^2}{2R}(\hat{\imath} - \hat{\jmath})\right)$$ $$\vec{a}_{P,n} = \left(-\frac{v_0^2}{R} + \frac{v_0^2}{2R}\right)\hat{\imath} - \frac{v_0^2}{2R}\hat{\jmath}$$ $$\vec{a}_{P,n} = -\frac{v_0^2}{2R}\hat{\imath} - \frac{v_0^2}{2R}\hat{\jmath} = -\frac{v_0^2}{2R}(\hat{\imath} + \hat{\jmath})$$