Source: Physics Competition - Mechanics
Problem
Four children, A, B, C, and D, are at the vertices of a square, playing a chase game at the same constant speed $v$. A chases B, B chases C, C chases D, and D chases A. Each child always moves directly towards their target. At a certain instant, the four children form a square of side length $l$.
- After how much more time will the children catch their targets?
- What is the distance each child runs from that moment until they meet?
- What is the magnitude of each child's acceleration at that instant?
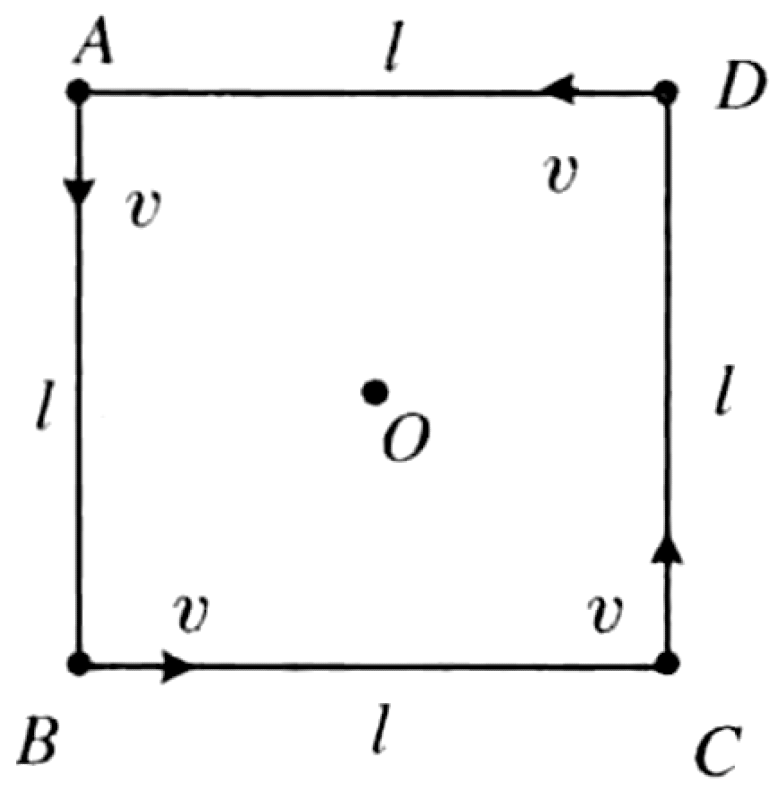
01K4K9790C3VDP95TNYVBMSZX1
[Q1] The time to meet is $t = \frac{l}{v}$. [Q2] The distance each child runs is $d = l$. [Q3] The magnitude of each child's acceleration is $a = \frac{v^2}{l}$.
This problem can be solved by analyzing the relative motion of the children and the geometry of their configuration, which remains a square that shrinks and rotates over time.
[Q1] After how much more time will the children catch their targets?
Consider the motion of child A chasing child B. The velocity of A, $\vec{v}_A$, points directly towards B. The velocity of B, $\vec{v}_B$, points towards C. At the instant shown, the line AB is perpendicular to the line BC.
The rate at which the distance $l$ between A and B decreases is the relative speed of approach along the line connecting them. This is the component of A's velocity along AB minus the component of B's velocity along AB.
- Component of $\vec{v}_A$ along AB: $v$
- Component of $\vec{v}_B$ along AB: $v \cos(90^\circ) = 0$
The speed of approach, $v_{\text{approach}}$, is constant:
$$v_{\text{approach}} = v - 0 = v$$Since the initial separation is $l$ and the speed of approach is constant, the time $t$ until they meet is:
$$t = \frac{\text{distance}}{\text{speed of approach}} = \frac{l}{v}$$[Q2] What is the distance each child runs from that moment until they meet?
Each child moves at a constant speed $v$ for the time $t = l/v$. The distance $d$ run by each child is the product of their speed and the time.
$$d = v \cdot t = v \left(\frac{l}{v}\right)$$ $$d = l$$[Q3] What is the magnitude of each child's acceleration at that instant?
Acceleration is the rate of change of the velocity vector, $\vec{a} = d\vec{v}/dt$. Since the speed $v$ is constant, the acceleration is entirely due to the change in the direction of the velocity. This is a form of centripetal acceleration.
Consider child B, whose velocity vector $\vec{v}_B$ always points towards C. The direction of $\vec{v}_B$ changes as C moves. The rate of change of the direction of $\vec{v}_B$ is equal to the angular velocity, $\omega$, of the line segment BC.
The angular velocity of BC is determined by the motion of C relative to B. At the given instant, C's velocity $\vec{v}_C$ is perpendicular to the line segment BC. The magnitude of C's velocity is $v$. The angular velocity of C about B is given by:
$$\omega = \frac{v_{\perp}}{r} = \frac{v}{l}$$where $v_{\perp}$ is the component of C's velocity perpendicular to BC, and $r$ is the distance BC.
The acceleration of an object moving at a constant speed $v$ whose velocity vector rotates with angular velocity $\omega$ has a magnitude:
$$a = v\omega$$Substituting the expression for $\omega$:
$$a = v \left(\frac{v}{l}\right) = \frac{v^2}{l}$$This is the magnitude of each child's acceleration at that instant.