Source: Physics Competition - Mechanics
Problem Sets:
Problem
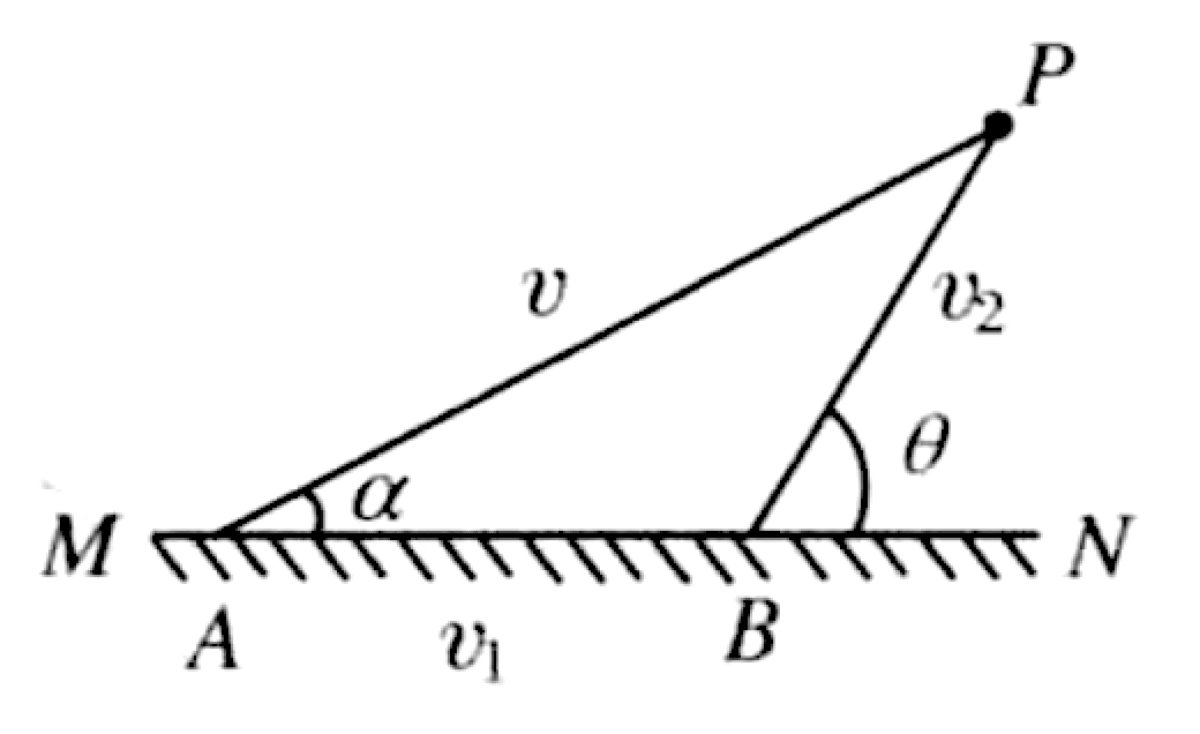
The lakeshore MN is a straight line. A small boat starts from point A on the shore and travels into the lake at a constant speed, at an angle $\alpha = 15^\circ$ with the shore. At the same time, a person also starts from point A. The person first runs along the shore for some distance and then swims in the water to chase the boat. The person's running speed on the shore is $v_1 = 4$ m/s, and their swimming speed in the water is $v_2 = 2$ m/s.
01K4H13QV3GF7YY82TNVZ6S9QY
The maximum speed the boat can have is given by the formula:
$$ v_{max} = \frac{v_1 v_2}{v_2 \cos \alpha + \sqrt{v_1^2 - v_2^2} \sin \alpha} $$Substituting the given values:
$$ v_{max} = 2\sqrt{2} \, \text{m/s} \approx 2.83 \, \text{m/s} $$To solve this problem, we must find the optimal path for the person to intercept the boat in the minimum possible time. The maximum speed of the boat, $v_{max}$, is such that the time it takes for the boat to reach the interception point P is equal to this minimum time for the person.
1. Optimal Path for the Person Let the person run from A to B and then swim from B to P, intercepting the boat at point P. The total time for the person is $t_{person} = t_{AB} + t_{BP} = \frac{AB}{v_1} + \frac{BP}{v_2}$. For a given interception point P, the person must choose point B on the shore to minimize this time. This is analogous to Fermat's principle for light refraction. The condition for the minimum time is that the angle of swimming, $\theta$, with respect to the shore satisfies:
$$ \cos \theta = \frac{v_2}{v_1} $$For a path to be optimal, the time saved by running an infinitesimal extra distance $dx$ along the shore must be balanced by the extra time taken to swim. This leads to the condition above, which holds for any viable interception. If $v_2 > v_1$, the person should swim directly from A. Here, $v_2 < v_1$, so this mixed path is possible.
2. Kinematic Condition for Interception Let the interception occur at time $t$. The distance traveled by the boat is $AP = vt$. The time taken by the person following the optimal path is $t_{person, min}$. For the limiting case of maximum boat speed, $v_{max}$, we have:
$$t = \frac{AP}{v_{max}} = t_{person, min} = \frac{AB}{v_1} + \frac{BP}{v_2}$$3. Geometric Analysis Consider the triangle ABP. The angles are:
- $\angle PAB = \alpha$
- $\angle ABP = 180^\circ - \theta$
- $\angle APB = 180^\circ - \alpha - (180^\circ - \theta) = \theta - \alpha$
Using the Law of Sines on triangle ABP:
$$ \frac{AB}{\sin(\theta - \alpha)} = \frac{BP}{\sin \alpha} = \frac{AP}{\sin(180^\circ - \theta)} = \frac{AP}{\sin \theta} $$From this, we express the path lengths $AB$ and $BP$ in terms of $AP$:
$$ AB = AP \frac{\sin(\theta - \alpha)}{\sin \theta} $$ $$ BP = AP \frac{\sin \alpha}{\sin \theta} $$4. Derivation of Maximum Speed Substitute these expressions into the time equality:
$$ \frac{AP}{v_{max}} = \frac{1}{v_1} \left( AP \frac{\sin(\theta - \alpha)}{\sin \theta} \right) + \frac{1}{v_2} \left( AP \frac{\sin \alpha}{\sin \theta} \right) $$Canceling $AP$ from both sides:
$$ \frac{1}{v_{max}} = \frac{\sin(\theta - \alpha)}{v_1 \sin \theta} + \frac{\sin \alpha}{v_2 \sin \theta} $$Using the angle subtraction formula $\sin(\theta - \alpha) = \sin\theta \cos\alpha - \cos\theta \sin\alpha$:
$$ \frac{1}{v_{max}} = \frac{\sin\theta \cos\alpha - \cos\theta \sin\alpha}{v_1 \sin \theta} + \frac{\sin \alpha}{v_2 \sin \theta} $$ $$ \frac{1}{v_{max}} = \frac{\cos \alpha}{v_1} - \frac{\cos \theta \sin \alpha}{v_1 \sin \theta} + \frac{\sin \alpha}{v_2 \sin \theta} = \frac{\cos \alpha}{v_1} + \sin \alpha \left( \frac{1}{v_2 \sin \theta} - \frac{\cos \theta}{v_1 \sin \theta} \right) $$Now, we use the optimal path condition, $\cos \theta = v_2 / v_1$. From this, we find $\sin \theta$:
$$ \sin \theta = \sqrt{1 - \cos^2 \theta} = \sqrt{1 - \left(\frac{v_2}{v_1}\right)^2} = \frac{\sqrt{v_1^2 - v_2^2}}{v_1} $$Substitute $\cos \theta$ and $\sin \theta$ into the equation for $1/v_{max}$:
$$ \frac{1}{v_{max}} = \frac{\cos \alpha}{v_1} + \sin \alpha \left( \frac{1}{v_2 \frac{\sqrt{v_1^2 - v_2^2}}{v_1}} - \frac{v_2/v_1}{v_1 \frac{\sqrt{v_1^2 - v_2^2}}{v_1}} \right) $$ $$ \frac{1}{v_{max}} = \frac{\cos \alpha}{v_1} + \frac{\sin \alpha}{\frac{\sqrt{v_1^2 - v_2^2}}{v_1}} \left( \frac{1}{v_2} - \frac{v_2}{v_1^2} \right) $$ $$ \frac{1}{v_{max}} = \frac{\cos \alpha}{v_1} + \frac{v_1 \sin \alpha}{\sqrt{v_1^2 - v_2^2}} \left( \frac{v_1^2 - v_2^2}{v_1^2 v_2} \right) $$ $$ \frac{1}{v_{max}} = \frac{\cos \alpha}{v_1} + \frac{\sin \alpha \sqrt{v_1^2 - v_2^2}}{v_1 v_2} $$ $$ \frac{1}{v_{max}} = \frac{v_2 \cos \alpha + \sqrt{v_1^2 - v_2^2} \sin \alpha}{v_1 v_2} $$The maximum speed of the boat is:
$$ v_{max} = \frac{v_1 v_2}{v_2 \cos \alpha + \sqrt{v_1^2 - v_2^2} \sin \alpha} $$5. Numerical Calculation Given values: $v_1 = 4$ m/s, $v_2 = 2$ m/s, $\alpha = 15^\circ$.
$$ \sqrt{v_1^2 - v_2^2} = \sqrt{4^2 - 2^2} = \sqrt{12} = 2\sqrt{3} \, \text{m/s} $$The trigonometric values for $15^\circ$ are:
$$ \cos 15^\circ = \frac{\sqrt{6} + \sqrt{2}}{4}, \quad \sin 15^\circ = \frac{\sqrt{6} - \sqrt{2}}{4} $$Substitute these into the expression for $v_{max}$:
$$ v_{max} = \frac{(4)(2)}{2 \left(\frac{\sqrt{6} + \sqrt{2}}{4}\right) + 2\sqrt{3} \left(\frac{\sqrt{6} - \sqrt{2}}{4}\right)} $$ $$ v_{max} = \frac{8}{\frac{\sqrt{6} + \sqrt{2}}{2} + \frac{\sqrt{18} - \sqrt{6}}{2}} = \frac{16}{\sqrt{6} + \sqrt{2} + 3\sqrt{2} - \sqrt{6}} $$ $$ v_{max} = \frac{16}{4\sqrt{2}} = \frac{4}{\sqrt{2}} = 2\sqrt{2} \, \text{m/s} $$