Source: Physics Competition - Mechanics
Problem Sets:
Problem
An object is launched from the base of a triangular prism resting on a horizontal surface. The left face of the prism has an inclination angle of $\theta$ with the horizontal, and the right face has an inclination angle of $\varphi$. The object is launched with an angle $\alpha$ relative to the horizontal from the bottom corner of the $\theta$-inclined face. The trajectory is such that the object just grazes the peak of the prism and lands at the bottom corner of the $\varphi$-inclined face.
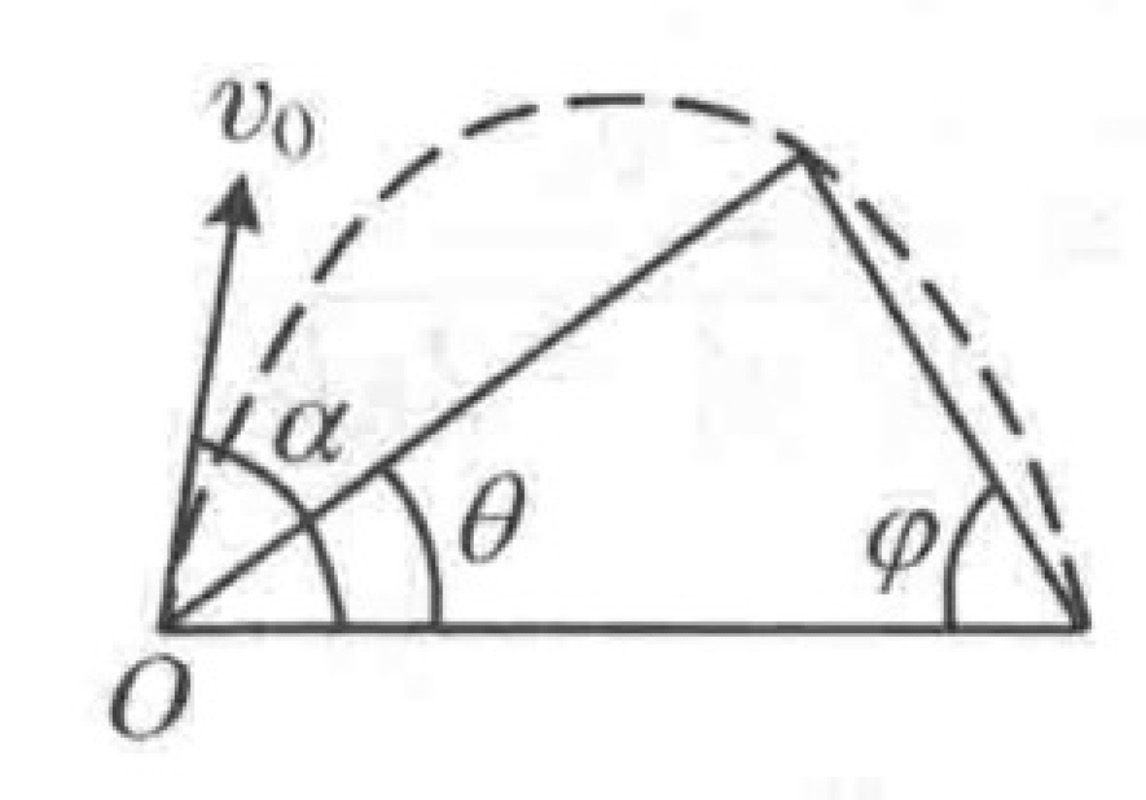
The relationship between the launch angle $\alpha$ and the inclination angles $\theta$ and $\varphi$ is:
$$\tan \alpha = \tan \theta + \tan \varphi$$Let the launch point be the origin (0, 0) of a Cartesian coordinate system. The trajectory of the projectile is given by the equation:
$$y(x) = x \tan \alpha - \frac{g}{2v_0^2 \cos^2\alpha} x^2$$where $\alpha$ is the launch angle, $v_0$ is the initial speed, and $g$ is the acceleration due to gravity.
The projectile lands at the base of the $\varphi$-inclined face. Let the total horizontal range be $R$. The landing point is $(R, 0)$. Substituting this into the trajectory equation:
$$0 = R \tan \alpha - \frac{gR^2}{2v_0^2 \cos^2\alpha}$$For $R eq 0$, we can express the constant term as:
$$\frac{g}{2v_0^2 \cos^2\alpha} = \frac{\tan \alpha}{R}$$Substituting this back into the general trajectory equation provides a simplified form that is independent of $v_0$:
$$y(x) = x \tan \alpha - x^2 \frac{\tan \alpha}{R} = x \tan \alpha \left(1 - \frac{x}{R}\right)$$Let the coordinates of the peak of the prism be $(x_P, y_P)$. This point lies on the trajectory. The geometry of the double-inclined plane gives two relations for these coordinates:
- From the left face: $\tan \theta = \frac{y_P}{x_P} \implies y_P = x_P \tan \theta$
- From the right face: $\tan \varphi = \frac{y_P}{R - x_P} \implies y_P = (R - x_P) \tan \varphi$
Since the peak $(x_P, y_P)$ is on the parabolic path, it must satisfy the trajectory equation:
$$y_P = x_P \tan \alpha \left(1 - \frac{x_P}{R}\right)$$Substituting the first geometric relation, $y_P = x_P \tan \theta$, into this equation gives:
$$x_P \tan \theta = x_P \tan \alpha \left(1 - \frac{x_P}{R}\right)$$Assuming $x_P eq 0$, we can divide by $x_P$:
$$\tan \theta = \tan \alpha \left(1 - \frac{x_P}{R}\right)$$To find the ratio $\frac{x_P}{R}$, we equate the two geometric expressions for $y_P$:
$$x_P \tan \theta = (R - x_P) \tan \varphi$$ $$x_P \tan \theta = R \tan \varphi - x_P \tan \varphi$$ $$x_P(\tan \theta + \tan \varphi) = R \tan \varphi$$ $$\frac{x_P}{R} = \frac{\tan \varphi}{\tan \theta + \tan \varphi}$$Finally, substitute this ratio back into the equation relating the angles:
$$\tan \theta = \tan \alpha \left(1 - \frac{\tan \varphi}{\tan \theta + \tan \varphi}\right)$$ $$\tan \theta = \tan \alpha \left(\frac{\tan \theta + \tan \varphi - \tan \varphi}{\tan \theta + \tan \varphi}\right)$$ $$\tan \theta = \tan \alpha \left(\frac{\tan \theta}{\tan \theta + \tan \varphi}\right)$$Assuming $\theta eq 0$, we can divide both sides by $\tan \theta$:
$$1 = \frac{\tan \alpha}{\tan \theta + \tan \varphi}$$This yields the final relationship between the angles:
$$\tan \alpha = \tan \theta + \tan \varphi$$