Source: Physics Competition - Mechanics
Problem Sets:
Problem
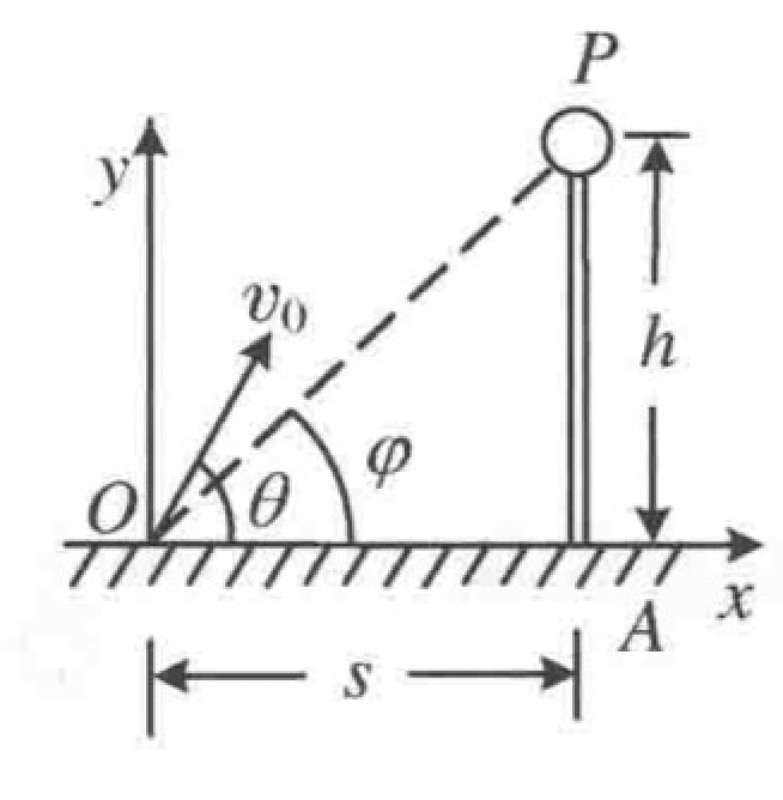
As shown in the figure, an object P is located at the top of a flagpole of height $h$. A boy at point O, a horizontal distance $s$ from the base of the flagpole A, shoots a small stone with a slingshot to hit the object P. The initial speed of the stone is $v_0$.
- What is the minimum value of the initial speed $v_0$ required for the stone to hit object P?
- What is the corresponding launch angle $\theta$ (the angle between the launch direction and the horizontal)?
[Q1] The minimum initial speed required is:
$$v_{0,min} = \sqrt{g(h + \sqrt{h^2+s^2})}$$[Q2] The corresponding launch angle $\theta$ is given by:
$$\tan\theta = \frac{h + \sqrt{h^2+s^2}}{s}$$The motion of the stone is projectile motion. We set up a coordinate system with the origin O at the launch point. The horizontal and vertical positions of the stone at time $t$ are given by:
$$x(t) = (v_0 \cos\theta) t$$ $$y(t) = (v_0 \sin\theta) t - \frac{1}{2}gt^2$$To hit the target P at coordinates $(s, h)$, we set $x(t) = s$ and $y(t) = h$. From the horizontal motion equation, we find the time of flight $t$:
$$s = (v_0 \cos\theta) t \implies t = \frac{s}{v_0 \cos\theta}$$Substitute this time into the vertical motion equation:
$$h = (v_0 \sin\theta) \left( \frac{s}{v_0 \cos\theta} \right) - \frac{1}{2}g \left( \frac{s}{v_0 \cos\theta} \right)^2$$ $$h = s \tan\theta - \frac{gs^2}{2v_0^2 \cos^2\theta}$$Using the identity $1/\cos^2\theta = 1 + \tan^2\theta$, we obtain the trajectory equation relating the launch speed $v_0$ and angle $\theta$ to the target coordinates:
$$h = s \tan\theta - \frac{gs^2}{2v_0^2}(1 + \tan^2\theta)$$To find the minimum speed, we rearrange this into a quadratic equation for $\tan\theta$:
$$\left(\frac{gs^2}{2v_0^2}\right) \tan^2\theta - s \tan\theta + \left(h + \frac{gs^2}{2v_0^2}\right) = 0$$For a real solution for $\tan\theta$ (and thus a real launch angle $\theta$) to exist, the discriminant of this quadratic equation must be non-negative ($\Delta \ge 0$).
$$\Delta = (-s)^2 - 4 \left(\frac{gs^2}{2v_0^2}\right) \left(h + \frac{gs^2}{2v_0^2}\right) \ge 0$$ $$s^2 - \frac{2gs^2h}{v_0^2} - \frac{g^2s^4}{v_0^4} \ge 0$$Since $s eq 0$, we can divide by $s^2$ and multiply by $v_0^4$ (which is positive) to clear the denominators:
$$v_0^4 - 2ghv_0^2 - g^2s^2 \ge 0$$The minimum initial speed, $v_{0,min}$, is the value for which the equality holds, corresponding to the case where there is only one possible launch angle ($\Delta = 0$). We solve the quadratic equation for $v_{0,min}^2$:
$$v_{0,min}^4 - 2ghv_{0,min}^2 - g^2s^2 = 0$$ $$v_{0,min}^2 = \frac{2gh \pm \sqrt{(-2gh)^2 - 4(1)(-g^2s^2)}}{2} = gh \pm g\sqrt{h^2 + s^2}$$Since $v_{0,min}^2$ must be positive, we take the positive root:
$$v_{0,min}^2 = g(h + \sqrt{h^2+s^2})$$[Q1] The minimum initial speed is:
$$v_{0,min} = \sqrt{g(h + \sqrt{h^2+s^2})}$$[Q2] For this minimum speed, the discriminant is zero, and the quadratic equation for $\tan\theta$ has a single solution:
$$\tan\theta = \frac{-(-s)}{2(gs^2/2v_{0,min}^2)} = \frac{s v_{0,min}^2}{gs^2} = \frac{v_{0,min}^2}{gs}$$Substituting the expression for $v_{0,min}^2$:
$$\tan\theta = \frac{g(h + \sqrt{h^2+s^2})}{gs} = \frac{h + \sqrt{h^2+s^2}}{s}$$The corresponding launch angle is $\theta = \arctan\left(\frac{h + \sqrt{h^2+s^2}}{s}\right)$.