Source: Principles of Physics
Problem Sets:
Problem
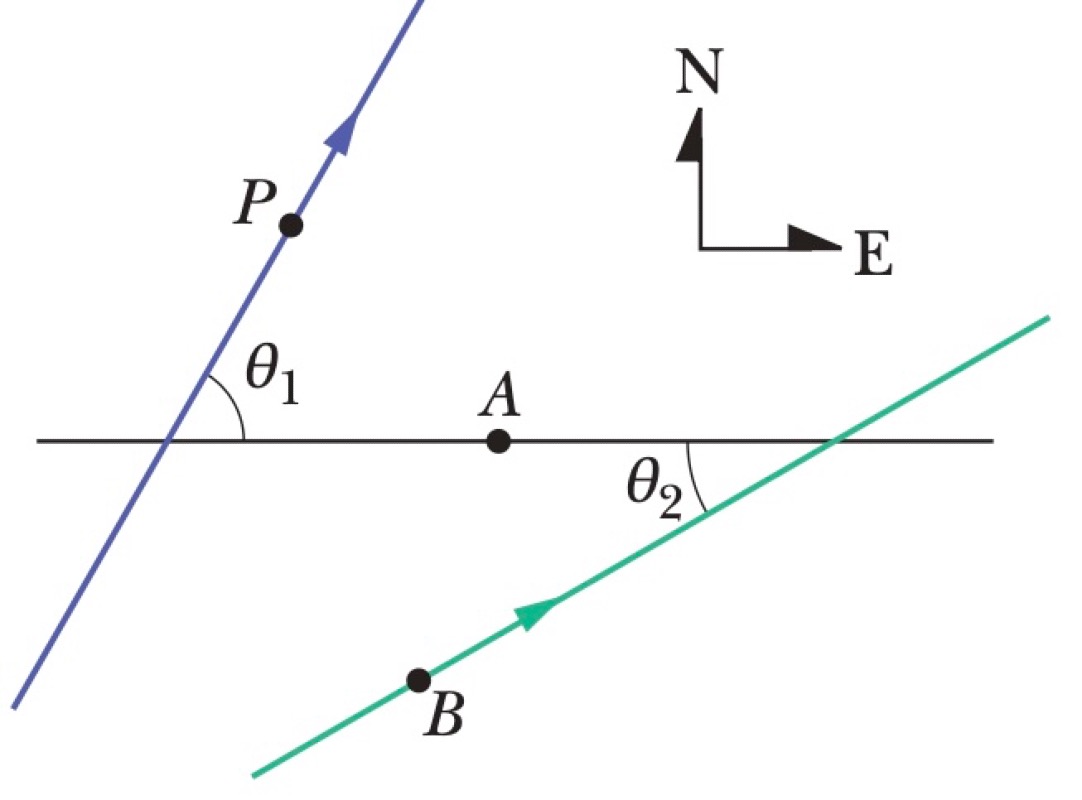
In an overhead view, two jeeps, P and B, race past a stationary observer A. Let East be the positive x-direction and North be the positive y-direction. Relative to observer A, jeep B travels at a constant speed $v_B$ at an angle $\theta_2$ south of east. Relative to observer A, jeep P accelerates from rest at a constant rate $a_P$ at an angle $\theta_1$ north of east. At a certain time, jeep P has a speed $v_P$.
- What is the magnitude of the velocity of P relative to B at that time?
- What is the direction of the velocity of P relative to B at that time?
- What is the magnitude of the acceleration of P relative to B?
- What is the direction of the acceleration of P relative to B?
[Q1] $|\vec{v}_{PB}| = \sqrt{v_P^2 + v_B^2 - 2v_P v_B \cos(\theta_1 + \theta_2)}$ [Q2] $\phi_v = \arctan\left(\frac{v_P \sin\theta_1 + v_B \sin\theta_2}{v_P \cos\theta_1 - v_B \cos\theta_2}\right)$ north of east [Q3] $|\vec{a}_{PB}| = a_P$ [Q4] $\theta_1$ north of east
We define the kinematic vectors in a Cartesian coordinate system (East $\hat{i}$, North $\hat{j}$). All angles are measured from the East axis.
The velocity of jeep P is $\vec{v}_P = (v_P \cos\theta_1)\hat{i} + (v_P \sin\theta_1)\hat{j}$. The velocity of jeep B is $\vec{v}_B = (v_B \cos\theta_2)\hat{i} - (v_B \sin\theta_2)\hat{j}$.
The velocity of P relative to B is $\vec{v}_{PB} = \vec{v}_P - \vec{v}_B$.
$$ \vec{v}_{PB} = (v_P \cos\theta_1 - v_B \cos\theta_2)\hat{i} + (v_P \sin\theta_1 + v_B \sin\theta_2)\hat{j} $$The magnitude $|\vec{v}_{PB}|$ is found using the Pythagorean theorem on its components. Expanding and simplifying using trigonometric identities:
$$ |\vec{v}_{PB}| = \sqrt{(v_P \cos\theta_1 - v_B \cos\theta_2)^2 + (v_P \sin\theta_1 + v_B \sin\theta_2)^2} $$ $$ |\vec{v}_{PB}| = \sqrt{v_P^2(\cos^2\theta_1+\sin^2\theta_1) + v_B^2(\cos^2\theta_2+\sin^2\theta_2) - 2v_P v_B(\cos\theta_1\cos\theta_2 - \sin\theta_1\sin\theta_2)} $$ $$ |\vec{v}_{PB}| = \sqrt{v_P^2 + v_B^2 - 2v_P v_B \cos(\theta_1 + \theta_2)} $$The direction angle $\phi_v$ of $\vec{v}_{PB}$ relative to the East axis is:
$$ \phi_v = \arctan\left(\frac{v_{PB,y}}{v_{PB,x}}\right) $$The acceleration of jeep P is $\vec{a}_P = (a_P \cos\theta_1)\hat{i} + (a_P \sin\theta_1)\hat{j}$. The acceleration of jeep B is $\vec{a}_B = \vec{0}$ since its velocity is constant.
The acceleration of P relative to B is $\vec{a}_{PB} = \vec{a}_P - \vec{a}_B = \vec{a}_P$. Therefore, the magnitude of the relative acceleration is simply $a_P$, and its direction is $\theta_1$ north of east.