Source: Principles of Physics
Problem Sets:
Problem
A ball is thrown, landing on a roof a time $t$ later. The landing spot is at a height $h$ above the launch point. Just before landing, the ball's path makes an angle $\theta$ with the horizontal roof. Assume the acceleration due to gravity is $g$ and that the ball is descending when it lands.
- Find the horizontal distance $d$ it travels.
- What is the magnitude of the ball's initial velocity, $v_0$?
- What is the angle $\alpha_0$ (relative to the horizontal) of the ball's initial velocity?
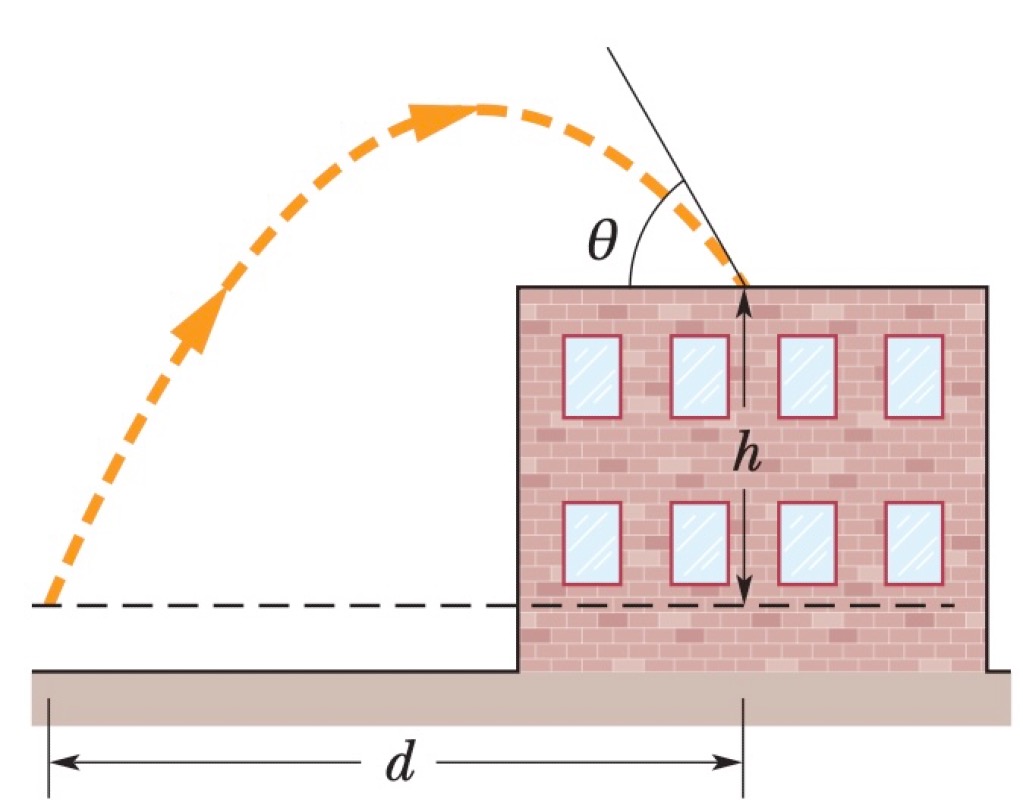
[Q1] $d = \frac{gt^2 - 2h}{2\tan\theta}$
[Q2] $v_0 = \frac{1}{2t}\sqrt{\left(\frac{gt^2 - 2h}{\tan\theta}\right)^2 + (gt^2 + 2h)^2}$
[Q3] $\alpha_0 = \arctan\left(\frac{(gt^2 + 2h)\tan\theta}{gt^2 - 2h}\right)$
Let the initial velocity be $\vec{v}_0 = (v_{0x}, v_{0y})$. The origin is at the launch point.
The vertical displacement is given by $h = v_{0y}t - \frac{1}{2}gt^2$. Solving for the initial vertical velocity component:
$$v_{0y} = \frac{h}{t} + \frac{1}{2}gt$$The final vertical velocity component is $v_{fy} = v_{0y} - gt$. Substituting the expression for $v_{0y}$:
$$v_{fy} = \left(\frac{h}{t} + \frac{1}{2}gt\right) - gt = \frac{h}{t} - \frac{1}{2}gt$$The horizontal velocity $v_{0x}$ is constant. The final angle $\theta$ relates the velocity components. Since the ball is descending, $|v_{fy}| = -v_{fy}$.
$$\tan\theta = \frac{|v_{fy}|}{v_{0x}} = \frac{-v_{fy}}{v_{0x}} = \frac{\frac{1}{2}gt - \frac{h}{t}}{v_{0x}}$$Solving for the initial horizontal velocity component:
$$v_{0x} = \frac{\frac{1}{2}gt - \frac{h}{t}}{\tan\theta}$$The required quantities are found using $v_{0x}$ and $v_{0y}$: The horizontal distance is $d = v_{0x}t$. The initial speed is $v_0 = \sqrt{v_{0x}^2 + v_{0y}^2}$. The initial angle is $\alpha_0 = \arctan(v_{0y}/v_{0x})$.