Source: Principles of Physics
Problem
A projectile is launched from an initial height $h_0$ and is later caught at the same height. It passes over a wall, first on its way up at time $t_1$ after launch, and again on its way down after an additional time interval $\Delta t$. The horizontal distance between the points where the projectile clears the wall is $D$.
- What is the total horizontal distance $R$ traveled by the projectile?
- What is the magnitude of the projectile's initial velocity, $v_0$?
- What is the angle $\theta_0$ (relative to the horizontal) of the projectile's initial velocity?
- What is the height $H$ of the wall, measured from the ground?
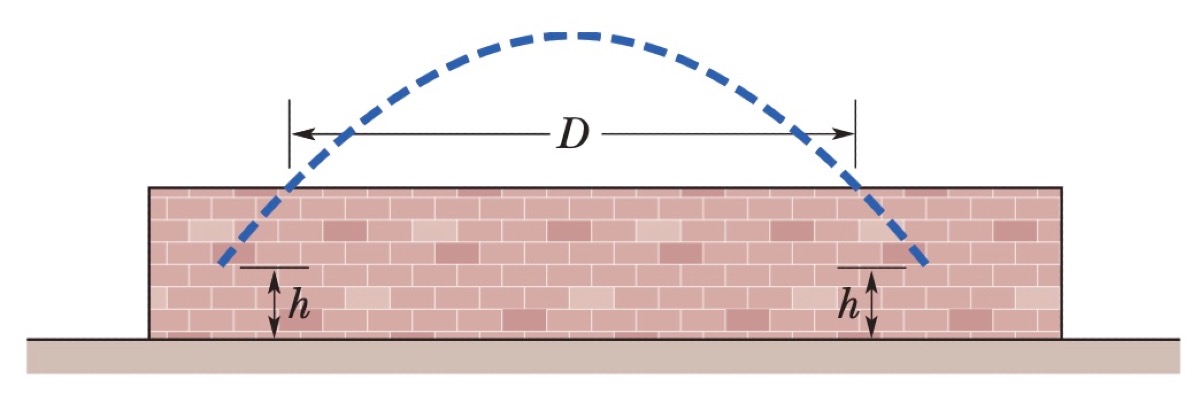
[Q1] $R = D\left(\frac{2t_1}{\Delta t} + 1\right)$ [Q2] $v_0 = \sqrt{\left(\frac{D}{\Delta t}\right)^2 + \frac{g^2}{4}(2t_1 + \Delta t)^2}$ [Q3] $\theta_0 = \arctan\left(\frac{g \Delta t (2t_1 + \Delta t)}{2D}\right)$ [Q4] $H = h_0 + \frac{1}{2}gt_1(t_1 + \Delta t)$
Let the origin $(0,0)$ be the launch point of the projectile. The initial velocity is $\vec{v}_0 = v_x \hat{i} + v_{0y} \hat{j}$. The acceleration is $\vec{a} = -g \hat{j}$.
The horizontal velocity $v_x$ is constant. The projectile travels a horizontal distance $D$ in the time interval $\Delta t$ while above the wall.
$$v_x = \frac{D}{\Delta t}$$The projectile is at the same vertical position (top of the wall) at time $t_1$ and at time $t_2 = t_1 + \Delta t$. By the symmetry of parabolic motion, the time to reach the peak height is the average of these two times:
$$t_{peak} = \frac{t_1 + t_2}{2} = \frac{t_1 + (t_1 + \Delta t)}{2} = t_1 + \frac{\Delta t}{2}$$At the peak of the trajectory, the vertical velocity is zero. Using $v_y(t) = v_{0y} - gt$:
$$v_y(t_{peak}) = v_{0y} - g t_{peak} = 0 \implies v_{0y} = g t_{peak} = g\left(t_1 + \frac{\Delta t}{2}\right)$$Since the projectile is caught at the same height it was launched, the total flight time $T$ is twice the time to reach the peak.
$$T = 2 t_{peak} = 2t_1 + \Delta t$$[Q1] The total horizontal distance (range) is $R = v_x T$.
$$R = \left(\frac{D}{\Delta t}\right)(2t_1 + \Delta t) = D\left(\frac{2t_1}{\Delta t} + 1\right)$$[Q2] The magnitude of the initial velocity is $v_0 = \sqrt{v_x^2 + v_{0y}^2}$.
$$v_0 = \sqrt{\left(\frac{D}{\Delta t}\right)^2 + \left(g\left(t_1 + \frac{\Delta t}{2}\right)\right)^2}$$[Q3] The angle of the initial velocity is $\theta_0 = \arctan(v_{0y}/v_x)$.
$$\theta_0 = \arctan\left(\frac{g(t_1 + \Delta t/2)}{D/\Delta t}\right) = \arctan\left(\frac{g \Delta t(2t_1 + \Delta t)}{2D}\right)$$[Q4] The height of the wall relative to the launch point, $y_{wall}$, is the projectile's vertical position at $t_1$.
$$y_{wall} = v_{0y}t_1 - \frac{1}{2}gt_1^2 = g\left(t_1 + \frac{\Delta t}{2}\right)t_1 - \frac{1}{2}gt_1^2 = \frac{1}{2}gt_1(2t_1 + \Delta t - t_1) = \frac{1}{2}gt_1(t_1 + \Delta t)$$The total height of the wall from the ground is $H = h_0 + y_{wall}$.
$$H = h_0 + \frac{1}{2}gt_1(t_1 + \Delta t)$$