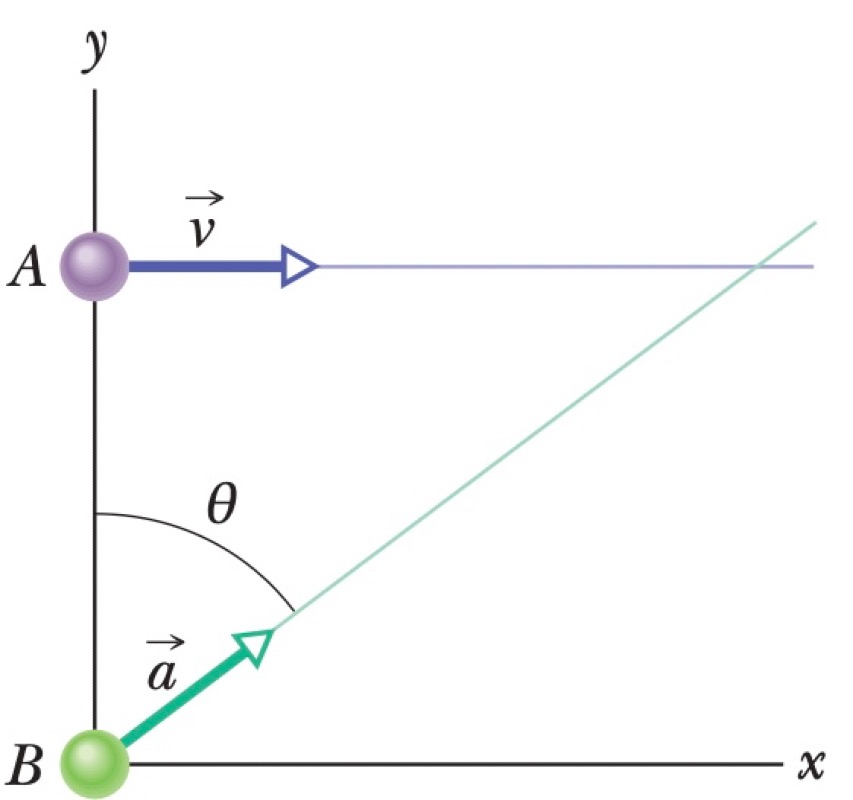
For a collision to occur at time $t_c$, the position vectors of the particles must be equal, $\vec{r}_A(t_c) = \vec{r}_B(t_c)$. The initial conditions are $\vec{r}_{A,0} = d\hat{j}$ and $\vec{r}_{B,0} = \vec{0}$.

The position of particle A at time $t$ is:

$$\vec{r}_A(t) = \vec{r}_{A,0} + \vec{v}t = (vt)\hat{i} + d\hat{j}$$

The position of particle B at time $t$ is:

$$\vec{r}_B(t) = \frac{1}{2}\vec{a}t^2 = \frac{1}{2} (a\sin\theta)\hat{i} t^2 + \frac{1}{2} (a\cos\theta)\hat{j} t^2$$

Equating the components at the collision time $t_c$:

$$x: vt_c = \frac{1}{2}at_c^2\sin\theta \implies t_c = \frac{2v}{a\sin\theta}$$ $$y: d = \frac{1}{2}at_c^2\cos\theta$$

Substitute the expression for $t_c$ from the x-component equation into the y-component equation:

$$d = \frac{1}{2}a\cos\theta \left( \frac{2v}{a\sin\theta} \right)^2 = \frac{2v^2\cos\theta}{a\sin^2\theta}$$

Rearrange and use the identity $\sin^2\theta = 1 - \cos^2\theta$ to form a quadratic equation for $\cos\theta$:

$$ad\sin^2\theta = 2v^2\cos\theta$$ $$ad(1 - \cos^2\theta) = 2v^2\cos\theta$$ $$ad\cos^2\theta + 2v^2\cos\theta - ad = 0$$

Solving the quadratic equation for $\cos\theta$ and choosing the positive root (since collision occurs in the first quadrant, $\theta \in (0, \pi/2)$):

$$\cos\theta = \frac{-2v^2 + \sqrt{(2v^2)^2 - 4(ad)(-ad)}}{2ad} = \frac{-v^2 + \sqrt{v^4 + a^2d^2}}{ad}$$