Source: Principles of Physics
Problem Sets:
Problem
A ball is shot vertically upward from the surface of a planet. A plot of its height $y$ versus time $t$ shows that it reaches a maximum height $y_{max}$ and has a total time of flight $T$ before returning to its starting height.
- What is the magnitude of the free-fall acceleration, $g_p$, on the planet?
- What is the magnitude of the initial velocity, $v_0$, of the ball?
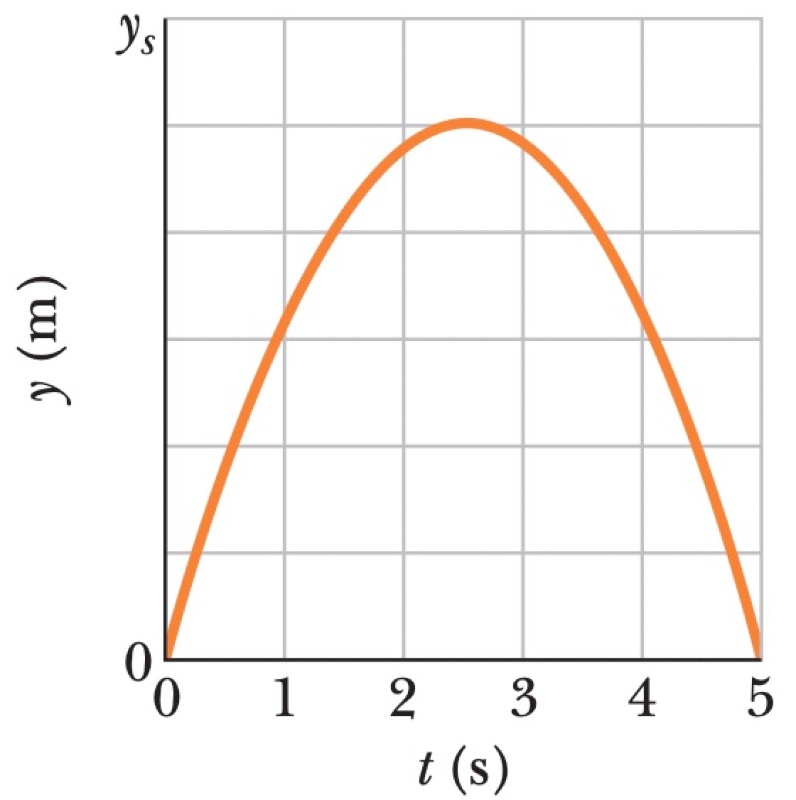
[Q1] $g_p = \frac{8 y_{max}}{T^2}$ [Q2] $v_0 = \frac{4 y_{max}}{T}$
The trajectory is symmetric, so the time to reach the maximum height is half the total flight time, $t_{peak} = T/2$. At the peak, the vertical velocity is zero.
To find the free-fall acceleration $g_p$, we consider the fall from rest at the peak. The ball travels a distance $y_{max}$ in a time $t_{peak}$. Using the kinematic equation for displacement:
$$y_{max} = \frac{1}{2} g_p t_{peak}^2 = \frac{1}{2} g_p \left(\frac{T}{2}\right)^2 = \frac{g_p T^2}{8}$$Solving for $g_p$:
$$g_p = \frac{8 y_{max}}{T^2}$$To find the initial velocity $v_0$, we consider the upward motion. The velocity becomes zero at time $t_{peak}$. Using the kinematic equation for velocity, $v_f = v_0 - g_p t$:
$$0 = v_0 - g_p t_{peak}$$ $$v_0 = g_p t_{peak} = \left(\frac{8 y_{max}}{T^2}\right) \left(\frac{T}{2}\right)$$Simplifying gives the initial velocity:
$$v_0 = \frac{4 y_{max}}{T}$$