Source: Principles of Physics
Problem Sets:
Problem
A particle moves along an x-axis with constant acceleration $a$. The accompanying figure shows the particle's position $x$ as a function of time $t$. The particle is at position $x_0$ at $t=0$, passes the origin at time $t=T$, and is at position $x_s$ at time $t=2T$. The initial position is related to the final scaled position by $x_0 = -x_s/N$, where $N$ is a positive constant determined by the graph's grid.
- What is the magnitude of the particle's acceleration?
- What is the direction of the particle's acceleration, assuming $x_s > 0$?
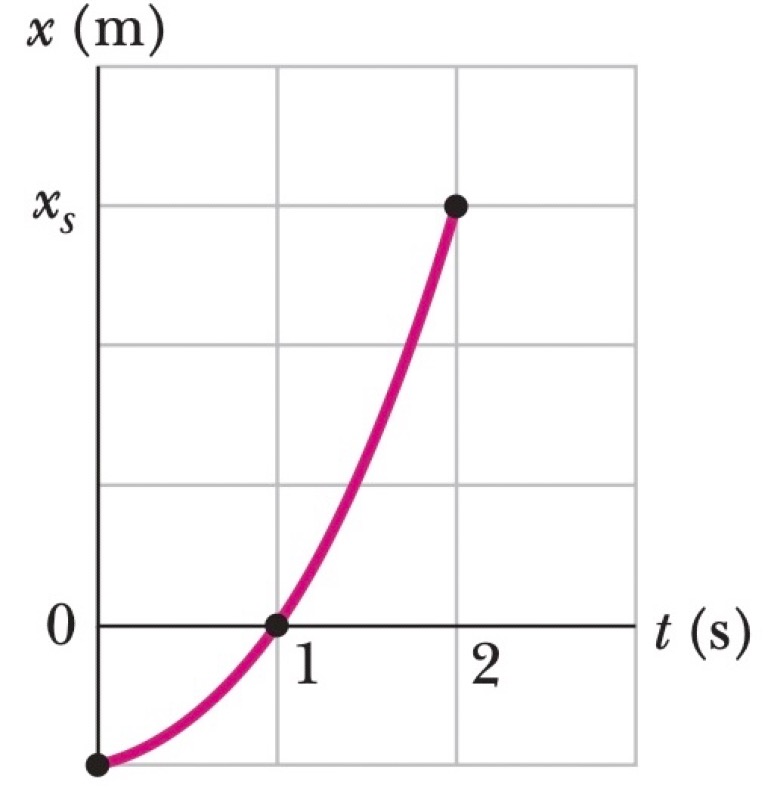
[Q1] $a = \frac{x_s(N-1)}{NT^2}$ [Q2] Positive x-direction
We analyze the particle's displacement over two consecutive time intervals of duration $T$.
The displacement in the first interval (from $t=0$ to $t=T$) is:
$$\Delta x_1 = x(T) - x(0) = 0 - x_0 = -x_0 = \frac{x_s}{N}$$The displacement in the second interval (from $t=T$ to $t=2T$) is:
$$\Delta x_2 = x(2T) - x(T) = x_s - 0 = x_s$$For motion with constant acceleration $a$, the difference in displacements over consecutive, equal time intervals is constant and given by $aT^2$.
$$\Delta x_2 - \Delta x_1 = aT^2$$Substituting the expressions for the displacements:
$$x_s - \frac{x_s}{N} = aT^2$$We can now solve for the acceleration $a$:
$$x_s\left(1 - \frac{1}{N}\right) = aT^2$$ $$a = \frac{x_s}{T^2}\frac{N-1}{N}$$For the given graph, $x_s>0$ and visually $N>1$, so the acceleration $a$ is positive. This means the acceleration is in the positive x-direction.